
3.在 
 ABCD中,设对角线
ABCD中,设对角线 =
= ,
,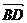 =
= 试用
试用 ,
,  表示
表示 ,
,
 解法一:
解法一: =
=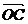 =
=

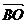 =
=
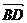 =
=

∴ =
= +
+ =
= -
-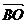 =
=
 -
-

 =
=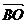 +
+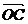 =
=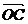 +
+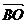 =
=
 +
+

解二:设 =
= ,
, =
=
则 +
+ =
= ,即
,即  +
+ =
= ;
;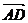 -
- =
=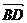 ,即
,即 -
- =
=
∴  =
= (
( -
- ),
),  =
= (
( +
+ )
)
即  =
= (
( -
- )
)
 =
= (
( +
+ )
)
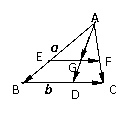
2.如图,在△ABC中, =
= ,
,  =
= ,AD为边BC的中线,G为△ABC的重心,求向量
,AD为边BC的中线,G为△ABC的重心,求向量
 解法一:∵
解法一:∵ =
= ,
,  =
= 则
则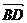 =
=
 =
=

∴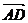 =
= +
+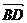 =
= +
+
 而
而 =
=
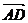
∴ =
=
 +
+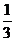

解法二:过G作BC的平行线,交AB、AC于E、F
∵△AEF∽△ABC,
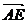 =
=
 =
=

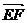 =
=
 =
=

 =
=
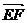 =
=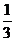

∴ =
=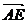 +
+ =
=
 +
+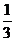

1.当λÎZ时,验证:λ( +
+ )=λ
)=λ +λ
+λ
证:当λ=0时,左边=0•( +
+ )=
)=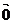 右边=0•
右边=0• +0•
+0• =
=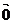 分配律成立
分配律成立
当λ为正整数时,令λ=n,
则有:n( +
+ )=(
)=( +
+ )+(
)+( +
+ )+…+(
)+…+( +
+ )
)
= +
+ +…+
+…+ +
+ +
+ +
+ +…+
+…+ =n
=n +n
+n
即λ为正整数时,分配律成立
当为负整数时,令λ=-n(n为正整数),有
-n( +
+ )=n[-(
)=n[-( +
+ )]=n[(-
)]=n[(- )+(-
)+(- )]=n(-
)]=n(- )+n(-
)+n(- )=-n
)=-n +(-n
+(-n )=-n
)=-n -n
-n
分配律仍成立
 综上所述,当λ为整数时,λ(
综上所述,当λ为整数时,λ( +
+ )=λ
)=λ +λ
+λ 恒成立
恒成立
2.用向量法解决几何问题
向量是数学中重要概念之一,是解决数学问题的得力工具,它简洁明快,许多几何里的命题,如果用向量知识来解决就显得格外简练.
 如图,MN是△ABC的中位线,求证:MN=
如图,MN是△ABC的中位线,求证:MN= BC,且MN∥BC.
BC,且MN∥BC.
证明:∵M、N分别是AB、AC边上的中点,所以 =
=
 ,
, =
=
 ,
, =
= -
- =
=
 -
-
 =
= (
( -
- )=
)=
 .
.
因此,NM= BC且MN∥BC.
BC且MN∥BC.
1.错例分析
判断向量a=-2e与b=2e是否共线?
对此题,有同学解答如下:
解:∵a=-2e,b=2e,∴b=-a,∴a与b共线.
分析:乍看上述解答,真是简单明快.然而,仔细研究题目已知,却发现
其解答存有问题,这是因为,原题已知中对向量e并无任何限制,那么就应允许e=0,而当e=0时,显然a=0,b=0,此时,a不符合定理中的条件,且使b=λa成立的λ值也不惟一(如λ=-1,λ=1,λ=2等均可使b=λa成立),故不能应用定理来判断它们是否共线.可见,对e=0的情况应另法判断才妥.
综上分析,此题应解答如下:
解:(1)当e=0时,则a=-2e=0
由于“零向量与任一向量平行”且“平行向量也是共线向量”,所以,此时a与b共线.
(2)当e≠0时,则a=-2e≠0,b=2e≠0
∴b=-a(这时满足定理中的a≠0,及有且只有一个实数λ(λ=-1),使得b=λa成立)
∴a与b共线.
综合(1)、(2)可知,a与b共线.
例1若3m+2n=a,m-3n=b,其中a,b是已知向量,求m,n.
分析:此题可把已知条件看作向量m、n的方程,通过方程组的求解获得m、n.
解:记3m+2n=a① m-3n=b②
3×②得3m-9n=3b③
①-③得11n=a-3b. ∴n=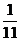 a-
a-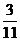 b④
b④
将④代入②有:m=b+3n=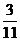 a+
a+ b
b
评述:在此题求解过程中,利用了实数与向量的积以及它所满足的交换律、结合律,从而解向量的二元一次方程组的方法与解实数的二元一次方程组的方法一致.
例2凸四边形ABCD的边AD、BC的中点分别为E、F,求证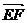 =
= (
( +
+ ).
).
解法一:构造三角形,使EF作为三角形中位线,借助于三角形中位线定理解决.
过点C在平面内作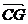 =
= ,则四边形ABGC是平行四边形,故F为AG中点.
,则四边形ABGC是平行四边形,故F为AG中点.
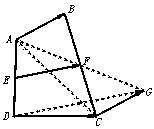 ∴EF是△ADG的中位线,∴EF =
∴EF是△ADG的中位线,∴EF = , ∴
, ∴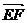 =
=
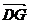 .
.
而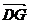 =
= +
+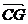 =
= +
+ ,
,
∴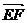 =
= (
( +
+ ).
).
解法二:创造相同起点,以建立向量间关系
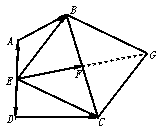 如图,连EB,EC,则有
如图,连EB,EC,则有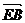 =
= +
+ ,
,
 =
=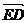 +
+ ,
,
又∵E是AD之中点,∴有 +
+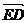 =0.
=0.
即有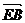 +
+ =
= +
+ ;
;
以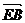 与
与 为邻边作平行四边形EBGC,则由F是BC之中点,可得F也是EG之中点.
为邻边作平行四边形EBGC,则由F是BC之中点,可得F也是EG之中点.
∴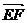 =
=
 =
= (
(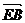 +
+ )=
)= (
( +
+ )
)
4.向量共线的充要条件
若有向量 (
( ¹
¹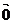 )、
)、 ,实数λ,使
,实数λ,使 =λ
=λ ,则
,则 与
与 为共线向量
为共线向量
若 与
与 共线(
共线( ¹
¹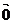 )且|
)且| |:|
|:| |=μ,则当
|=μ,则当 与
与 同向时
同向时 =μ
=μ ;
当
;
当 与
与 反向时
反向时 =-μ
=-μ 从而得
从而得
向量共线定理 向量 与非零向量
与非零向量 共线的充要条件是:有且只有一个非零实数λ,使
共线的充要条件是:有且只有一个非零实数λ,使 =λ
=λ
3.运算定律 结合律:λ(μ )=(λμ)
)=(λμ) ①
①
第一分配律:(λ+μ) =λ
=λ +μ
+μ ②
②
第二分配律:λ( +
+ )=λ
)=λ +λ
+λ ③
③
结合律证明:
如果λ=0,μ=0, =
=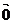 至少有一个成立,则①式成立
至少有一个成立,则①式成立
如果λ¹0,μ¹0, ¹
¹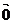 有:|λ(μ
有:|λ(μ )|=|λ||μ
)|=|λ||μ |=|λ||μ||
|=|λ||μ|| |
|
|(λμ) |=|λμ||
|=|λμ||  |=|λ||μ||
|=|λ||μ|| |
|
∴|λ(μ )|=|(λμ)
)|=|(λμ) |
|
如果λ、μ同号,则①式两端向量的方向都与 同向;
同向;
如果λ、μ异号,则①式两端向量的方向都与 反向
反向
从而λ(μ )=(λμ)
)=(λμ)
第一分配律证明:
如果λ=0,μ=0, =
=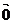 至少有一个成立,则②式显然成立
至少有一个成立,则②式显然成立
如果λ¹0,μ¹0, ¹
¹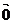
当λ、μ同号时,则λ 和μ
和μ 同向,
同向,
∴|(λ+μ) |=|λ+μ||
|=|λ+μ|| |=(|λ|+|μ|)|
|=(|λ|+|μ|)| |
|
|λ +μ
+μ |=|λ
|=|λ |+|μ
|+|μ |=|λ||
|=|λ|| |+|μ||
|+|μ|| |=(|λ|+|μ|)|
|=(|λ|+|μ|)| |
|
∵λ、μ同号 ∴②两边向量方向都与 同向
同向
即 |(λ+μ) |=|λ
|=|λ +μ
+μ |
|
当λ、μ异号,当λ>μ时 ②两边向量的方向都与λ 同向;当λ<μ时 ②两边向量的方向都与μ
同向;当λ<μ时 ②两边向量的方向都与μ 同向,且|(λ+μ)
同向,且|(λ+μ) |=|λ
|=|λ +μ
+μ |
|
∴②式成立
第二分配律证明:
如果 =
=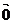 ,
, =
=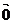 中至少有一个成立,或λ=0,λ=1则③式显然成立
中至少有一个成立,或λ=0,λ=1则③式显然成立
 当
当 ¹
¹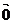 ,
, ¹
¹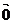 且λ¹0,λ¹1时
且λ¹0,λ¹1时
(1)当λ>0且λ¹1时在平面内任取一点O,
作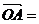

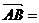

 λ
λ
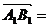 λ
λ
则
 +
+
 λ
λ +λ
+λ
由作法知 , ∥
∥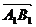 有ÐOAB=ÐOA1B1 |
有ÐOAB=ÐOA1B1 | |=λ|
|=λ|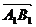 |
|
 ∴
∴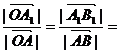 λ ∴△OAB∽△OA1B1
λ ∴△OAB∽△OA1B1
∴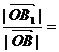 λ ÐAOB=Ð A1OB1
λ ÐAOB=Ð A1OB1
因此,O,B,B1在同一直线上,| |=|λ
|=|λ |
|  与λ
与λ 方向也相同
方向也相同
∴λ( +
+ )=λ
)=λ +λ
+λ
当λ<0时 可类似证明:λ( +
+ )=λ
)=λ +λ
+λ
∴ ③式成立
2.实数与向量的积:实数λ与向量 的积是一个向量,记作:λ
的积是一个向量,记作:λ
(1)|λ |=|λ||
|=|λ|| |
|
(2)λ>0时λ 与
与 方向相同;λ<0时λ
方向相同;λ<0时λ 与
与 方向相反;λ=0时λ
方向相反;λ=0时λ =
=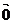
1. 示例:已知非零向量
示例:已知非零向量 ,作出
,作出 +
+ +
+ 和(-
和(- )+(-
)+(- )+(-
)+(- )
)
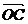 =
=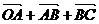 =
= +
+ +
+ =3
=3
 =
= =(-
=(- )+(-
)+(- )+(-
)+(- )=-3
)=-3
(1)3 与
与 方向相同且|3
方向相同且|3 |=3|
|=3| |;(2)-3
|;(2)-3 与
与 方向相反且|-3
方向相反且|-3 |=3|
|=3| |
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com