4．在一次信息技术考试中，某兴趣小组8名同学的成绩(单位：分)分别是：7，10，9，8，7，9，9，8， 则这组数据的众数是

　　 　A．7　 　　　　　B．8　　 　　　C．9　　 　　　　　　D．10

3．2010年5月27日，上海世博会参观人数达到37.7万人，37.7万用科学记数法表示应为

　 A． 0.377×l0⁶ 　　　B．3.77×l0⁵　 　C．3.77×l0⁴　　 　D．377×10³

2．计算的结果是

　 　A．a⁶　 　　　　　B．a⁵　 　　　　C．2a³　 　　　　　D．a

1．-(-2)的相反数是

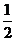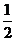　　A．2　 　　　　　B．　　 　　　C．-　 　　　　　D．-2

28．(本题满分10分)如图1是一个三棱柱包装盒，它的底面是边长为10cm的正三角形，三个

侧面都是矩形．现将宽为15cm的彩色矩形纸带AMCN裁剪成一个平行四边形ABCD(如

图2)，然后用这条平行四边形纸带按如图 3 的方式把这个三棱柱包装盒的侧面进行包贴

(要求包贴时没有重叠部分)，纸带在侧面缠绕三圈，正好将这个三棱柱包装盒的侧面全部

包贴满．本试卷由无锡市天一实验学校金杨建录制 QQ：623300747．转载请注明！

(1)请在图2中，计算裁剪的角度∠BAD；

(2)计算按图3方式包贴这个三棱柱包装盒所需的矩形纸带的长度．

27．(本题满分10分)如图，已知点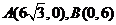，经过A、B的直线以每秒1个单位的

速度向下作匀速平移运动，与此同时，点P从点B出发,在直线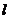上以每秒1个单位的速度沿直线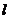向右下方向作匀速运动．设它们运动的时间为秒．

(1)用含的代数式表示点P的坐标；

(2)过O作OC⊥AB于C,过C作CD⊥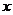轴

于D,问：为何值时,以P为圆心、1为半

径的圆与直线OC相切？并说明此时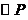

与直线CD的位置关系．

26．(本题满分10分)

(1)如图1，在正方形ABCD中，M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点，N是∠DCP的平分线上一点．若∠AMN=90°，求证：AM=MN．

下面给出一种证明的思路，你可以按这一思路证明，也可以选择另外的方法证明．

证明：在边AB上截取AE=MC，连ME．正方形ABCD中，∠B=∠BCD=90°，

AB=BC．∴∠NMC=180°-∠AMN­-∠AMB=180°-∠B-∠AMB=∠MAB

=∠MAE．本试卷由无锡市天一实验学校金杨建录制 QQ：623300747．转载请注明！

(下面请你完成余下的证明过程)

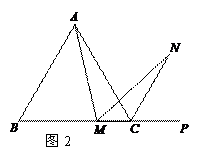(2)若将(1)中的“正方形ABCD”改为“正三角形ABC”(如图2),N是∠ACP的平分线上一点，则当∠AMN=60°时，结论AM=MN是否还成立？请说明理由．

本试卷由无锡市天一实验学校金杨建录制 QQ：623300747．转载请注明！

(3)若将(1)中的“正方形ABCD”改为“正边形ABCD…X”，请你作出猜想：当∠AMN

=　　　　　　　　 °时，结论AM=MN仍然成立．(直接写出答案，不需要证明)

25．(本题满分8分)某企业在生产甲、乙两种节能产品时需用A、B两种原料，生产每吨节能产品所需原料的数量如下表所示：

本试卷由无锡市天一实验学校金杨建录制 QQ：623300747．转载请注明！

销售甲、乙两种产品的利润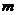(万元)与销售量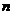(吨)之间的函数关系如图所示．已知

该企业生产了甲种产品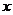吨和乙种产品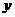吨，共用去A原料200吨．

(1)写出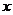与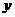满足的关系式；

(2)为保证生产的这批甲种、乙种产品售后的总利润不少于220万元，那么至少要用B原

料多少吨？

24．(本题满分10分)如图，矩形ABCD的顶点A、B的坐标分别为(-4,0)和(2,0)，BC=．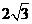

设直线AC与直线x=4交于点E．

(1)求以直线x=4为对称轴，且过C与原点O的抛物线的函数关系式,并说明此抛物线一定过点E；本试卷由无锡市天一实验学校金杨建录制 QQ：623300747．转载请注明！

(2)设(1)中的抛物线与x轴的另一个交点为N，

M是该抛物线上位于C、N之间的一动点，求

△CMN面积的最大值．

23．(本题满分8分)在东西方向的海岸线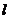上有一长为1km的码头MN(如图)，在码头西端

M 的正西19．5 km 处有一观察站A．某时刻测得一艘匀速直线航行的轮船位于 A 的北

偏西30°,且与A相距40km的B处；经过1小时20分钟，又测得该轮船位于A的北偏东

60°，且与A相距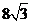km的C处．

(1)求该轮船航行的速度(保留精确结果)；

(2)如果该轮船不改变航向继续航行，那么轮船能否正

好行至码头MN靠岸？请说明理由．