
4、设非零向量 、
、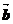 、
、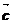 满足
满足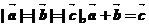 ,则
,则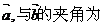 ( )
( )
A 150° B 30° C 60° D 120°
3、下列各式中,值为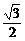 的是( )
的是( )
A.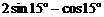 B.
B.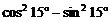
C.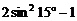 D.
D.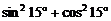
2、已知△ABC中,a= ,b=
,b=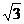 ,B=60°,那么角A等于( )
,B=60°,那么角A等于( )
A .135° B.90° C.30° D. 45°
1、若 ,
, , 则
, 则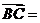 ( )
( )
A.(-1,-1) B.(1,1) C.(3,7) D.(-3,-7)
28.(2010江苏 镇江)深化理解(本小题满分9分)
对非负实数x“四舍五入”到个位的值记为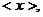
即:当n为非负整数时,如果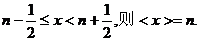
如:<0>=<0.48>=0,<0.64>=<1.493>=1,<2>=2,<3.5>=<4.12>=4,…
试解决下列问题:
(1)填空:①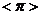 = (
= (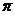 为圆周率);
为圆周率);
②如果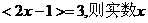 的取值范围为 ;
的取值范围为 ;
(2)①当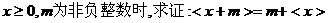 ;
;
②举例说明 不恒成立;
不恒成立;
(3)求满足 的值;
的值;
(4)设n为常数,且为正整数,函数 范围内取值时,函数值y为整数的个数记为
范围内取值时,函数值y为整数的个数记为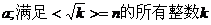 的个数记为b.
的个数记为b.
求证:
[答案](1)①3;(1分)② ; (2分)
; (2分)
(2)①证明:
[法一]设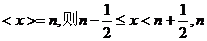 为非负整数; (3分)
为非负整数; (3分)
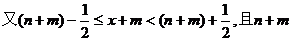 为非负整数,
为非负整数,
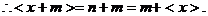 (4分)
(4分)
[法二]设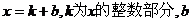 为其小数部分.
为其小数部分.
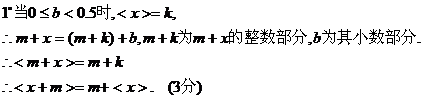

②举反例: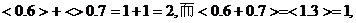
 不一定成立.(5分)
不一定成立.(5分)
(3)[法一]作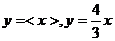 的图象,如图28 (6分)
的图象,如图28 (6分)
(注:只要求画出草图,如果没有把有关点画成空心点,不扣分)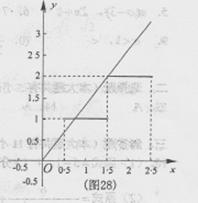

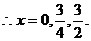 (7分)
(7分)
[法二]
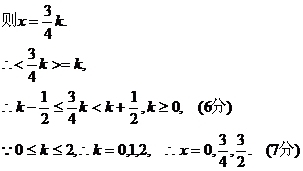
(4)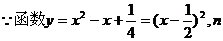 为整数,
为整数,
当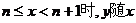 的增大而增大,
的增大而增大,
 , ①
, ①
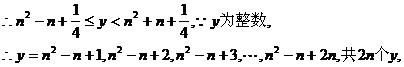
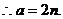 ② (8分)
② (8分)
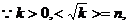
则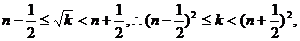 ③
③
比较①,②,③得: (9分)
(9分)
27.(2010江苏 镇江)探索发现(本小题满分9分)
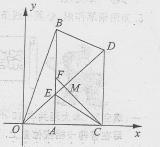
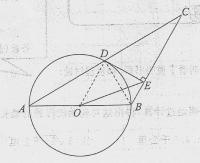
如图,在直角坐标系 的直角顶点A,C始终在x轴的正半轴上,B,D在第一象限内,点B在直线OD上方,OC=CD,OD=2,M为OD的中点,AB与OD相交于E,当点B位置变化时,
的直角顶点A,C始终在x轴的正半轴上,B,D在第一象限内,点B在直线OD上方,OC=CD,OD=2,M为OD的中点,AB与OD相交于E,当点B位置变化时,
试解决下列问题:
(1)填空:点D坐标为 ;
(2)设点B横坐标为t,请把BD长表示成关于t的函数关系式,并化简;
(3)等式BO=BD能否成立?为什么?
(4)设CM与AB相交于F,当△BDE为直角三角形时,判断四边形BDCF的形状,并证明你的结论.
[答案]
(1) ;(1分)
;(1分)
(2)
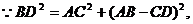
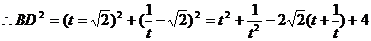 ① (2分)
① (2分)
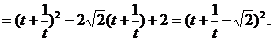 (3分)
(3分)
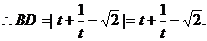 ② (4分)(注:不去绝
② (4分)(注:不去绝
对值符号不扣分)
(3)[法一]若OB=BD,则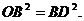
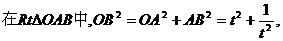
由①得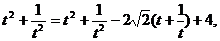 (5分)
(5分)

[法二]若OB=BD,则B点在OD的中垂线CM上.
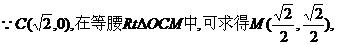
∴直线CM的函数关系式为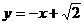 , ③ (5分)
, ③ (5分)
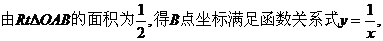 ④
④
联立③,④得: ,
,

[法三]若OB=BD,则B点在OD的中垂线CM上,如图27 – 1
过点B作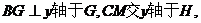


(4)如果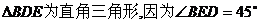 ,
,
①当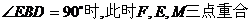 ,如图27 – 2
,如图27 – 2
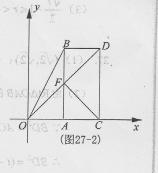
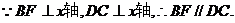
∴此时四边形BDCF为直角梯形.(7分)
②当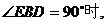 如图27 – 3
如图27 – 3
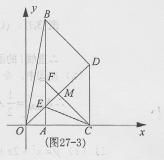
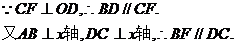
∴此时四边形BDCF为平行四边形.(8分)
下证平行四边形BDCF为菱形:
[法一]在 ,
,

[方法①] 上方
上方
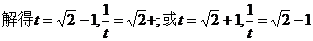 (舍去).
(舍去).
得
[方法②]由②得: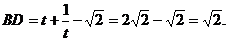
此时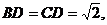
∴此时四边形BDCF为菱形(9分)
[法二]在等腰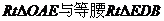 中
中
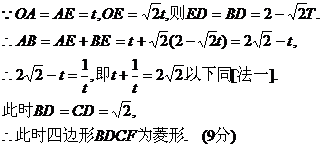
26.(2010 江苏镇江)推理证明(本小题满分7分)
如图,已知△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,过D作DE⊥BC,垂足为E,连结OE,CD=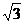 ,∠ACB=30°.
,∠ACB=30°.
(1)求证:DE是⊙O的切线;
(2)分别求AB,OE的长;
(3)填空:如果以点E为圆心,r为半径的圆上总存在不同的两点到点O的距离为1,则r的取值范围为 .
[答案](1)∵AB是直径,∴∠ADB=90° (1分)

∴OD⊥DE,∴DE是⊙O的切线. (3分)
(2)在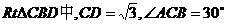 ,
,
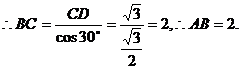 (4分)
(4分)
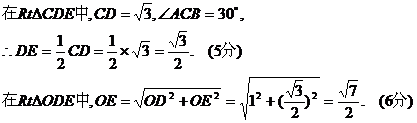
(3) (7分)
(7分)
25.(2010 江苏镇江)描述证明(本小题满分6分)
海宝在研究数学问题时发现了一个有趣的现象:

(1)请你用数学表达式补充完整海宝发现的这个有趣的现象;
(2)请你证明海宝发现的这个有趣现象.
[答案](1)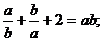 (1分)
(1分) (2分)
(2分)
(2)证明: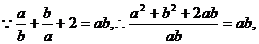 (3分)
(3分)
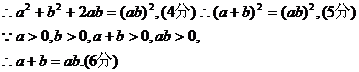
24.(2010 江苏镇江)实践应用(本小题满分6分)
有200名待业人员参加某企业甲、乙、丙三个部门的招聘,到各部门报名的人数百分比见图表1,该企业各部门的录取率见图表2.(部门录取率= ×100%)
×100%)

(1)到乙部门报名的人数有 人,乙部门的录取人数是 人,该企业的录取率为 ;
(2)如果到甲部门报名的人员中有一些人员改到丙部门报名,在保持各部门录取率不变的情况下,该企业的录取率将恰好增加15%,问有多少人从甲部门改到丙部门报名?
[答案](1)80,(1分)40,(2分) 47%;(3分)
(2)设有x人从甲部门改到丙部门报名,(4分)
则: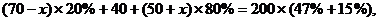 (5分)
(5分)
化简得:0.6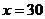 ,
,
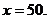
答:有50人从甲部门改到丙部门报名,恰好增加15%的录取率.(6分
23.(2010 江苏镇江)运算求解(本小题满分6分)
已知二次函数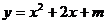 的图象C1与x轴有且只有一个公共点.
的图象C1与x轴有且只有一个公共点.
(1)求C1的顶点坐标;
(2)将C1向下平移若干个单位后,得抛物线C2,如果C2与x轴的一个交点为A(-3,0),求C2的函数关系式,并求C2与x轴的另一个交点坐标;
(3)若 的取值范围.
的取值范围.
[答案](1)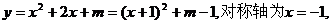 (1分)
(1分)
 轴有且只有一个公共点,∴顶点的纵坐标为0.
轴有且只有一个公共点,∴顶点的纵坐标为0.
∴C1的顶点坐标为(-1,0) (2分)
(2)设C2的函数关系式为
把A(-3,0)代入上式得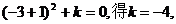
∴C2的函数关系式为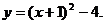 (3分)
(3分)
∵抛物线的对称轴为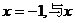 轴的一个交点为A(-3,0),由对称性可知,它与x轴的另一个交点坐标为(1,0). (4分)
轴的一个交点为A(-3,0),由对称性可知,它与x轴的另一个交点坐标为(1,0). (4分)
(3)当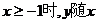 的增大而增大,
的增大而增大,
当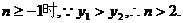 (5分)
(5分)
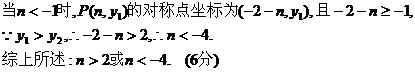
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com