
2.下列各组词语中没有错别字的一组是( ) A.怄气 前踞后恭 羽扇纶巾 不能框得太死 B.倏乎 横渡长江 戳穿阴谋 家在蛤蟆陵下住 C.涣散 嘉宾满座 拾人牙慧 金銮殿上坐皇帝 D.纷云 殚精竭虑 擢发难数 睃睁着眼睛发愣 3.下列各句中加点的成语中使用不恰当的一句是( ) A.这事你现在做不了,就不要勉为其难,以后有条件再做不迟。 B.他谦虚地说:"我既不擅长唱歌,也不喜欢运动;除了画画,就别无长物了。" C.随着再就业工程的实施,许多下岗职工坚信山不转水转,自立自强,重新找到了人生的位置。 D.在国企改革中,某些人"明修栈道,暗度陈仓",打着企业改制的幌子,侵吞国有资产。4.下列各句中,没有语病的一句是( ) A.2005年春节快到了,我们学校补完课已是临近年三十,在回家的路上我突然邂逅相遇
了我一位多年未见的老同学。 B.《决胜2005语文高考模拟试题冲刺卷》是本刊编辑部特邀全国高考一线资深特级、高
级语文教师,以最新的全国高考语文试题命题动态为依据,并聘请高考命题与阅卷专
家一同参与审定的一套权威模拟试题。 C.《中国教育报》开辟了刊登教学一线老师阐述自己在教学中,如何进行教学改革,如
何既让学生学到知识,又使学生学到做人的文章。 D.中国也有一部分有钱人,这些有钱人也非常看重旅游度假。从旅游的目的地来看,他们
大都以新、马、泰或欧洲各国的居多。
语文基础知识练习(三)
1.下列词语中加点字的读音完全不相同的一组是( ) A.悼念 泥淖 绰绰有余 掉以轻心 B.蝎子 谒见 歇斯底里 竭尽全力 C.洪水 供奉 哄堂大笑 烘云托月 D.汲水 吸取 岌岌可危 负笈从师
10.(2005广东)设函数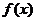 在
在 上满足
上满足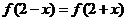 , f(7-x)=f(7+x),且在闭区间[0,7]上,只有f(1)=f(3)=0。
, f(7-x)=f(7+x),且在闭区间[0,7]上,只有f(1)=f(3)=0。
(Ⅰ)试判断函数y=f(x)的奇偶性;
(Ⅱ)试求方程f(x)=0在闭区间[-2005,2005]上的根的个数,并证明你的结论.
解:由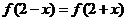 得
得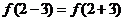 即
即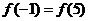
由已知易得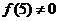 ,所以
,所以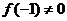 ,而
,而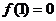 ,从而
,从而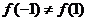 且
且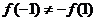
故函数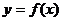 是非奇非偶函数;
是非奇非偶函数;
(II)由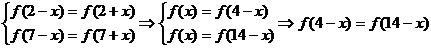
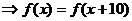 ,从而知函数
,从而知函数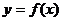 的周期为
的周期为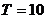
当 时,
时,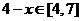 ,由已知
,由已知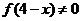 ,又
,又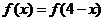 ,则
,则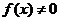
∴当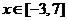 时,只有
时,只有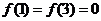
∴方程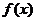 =0在一个周期内只有两个解
=0在一个周期内只有两个解
而函数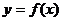 在闭区间[-2005,2005]共含有401个周期,所以方程
在闭区间[-2005,2005]共含有401个周期,所以方程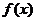 =0在闭区间[-2005,2005]共含有802个解
=0在闭区间[-2005,2005]共含有802个解
[探索题]对于k∈Z,用Ik表示区间(2k-1,2k+1]。已知x∈Ik时,f(x)= (x-2k)2,
(1)当k∈N*时,求集合Mk={a|使方程f(x)=ax在Ik上有两个不相等的实根的a的值}
(2)并讨论f(x)的周期性。
解:y=f(x)图像就是将y=x2(x∈(-1,1])向右平移2k个单位所得,其中k∈N
设y1=f(x),y2=ax,由集合Mk可知,若a∈M,则函数y1=f(x)与y2=ax图像有 两个交点,即当x=2k+1时,0<y2≤1
∴0<a≤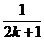
∴Mk={a|0<a≤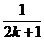 ,k∈N},即Mk=(0,
,k∈N},即Mk=(0,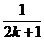 ]
]
对任意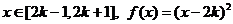
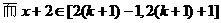
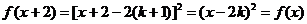 ,
,
所以f(x)是2为周期的周期函数。
思路点拔:化简集合,弄清图像变换规律,数形结合求解;周期性的的讨论注要是看你运用定义的意识和能力
9.设f(x)是定义在(-∞,+∞)上的函数,对一切x∈R均有f(x)+f(x+2)=0,当-1<x≤1时,f(x)=2x-1,求当1<x≤3时,函数f(x)的解析式。
思路分析:∵ f(x)+f(x+2)=0 ∴ f(x)=-f(x+2)
∵ 该式对一切x∈R成立,
∴ 以x-2代x得:f(x-2)=-f[(x-2)+2]=-f(x)
当1<x≤3时,-1<x-2≤1,∴ f(x-2)=2(x-2)-1=2x-5
∴ f(x)=-f(x-2)=-2x+5,∴ f(x)=-2x+5(1<x≤3)
评注:在化归过程中,一方面要转化自变量到已知解析式的定义域,另一方面要保持对应的函数值有一定关系。在化归过程中还体现了整体思想。
8.设f(x)为定义在实数集上周期为2的函数,且为偶函数,已知x∈[2,3]时f(x)=x,求x∈[-2,0]时f(x)的解析式。
分析:由T=2可得x∈[-2,-1]和x∈[0,1]时的解析式;再由奇偶性可得[-1,0]上的解析式。
解:因为函数f(x)是T=2的周期函数,所以f(x+2)=f(x).


又由于f(x)为偶函数,故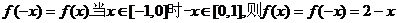
所以解析式为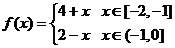
7.设函数f(x)的最小正周期为2002,并且f(1001+x)=f(1001-x)对一切x∈R均成立,试讨论f(x)的奇偶性.
解: ∵周期是2002, ∴ f(2002+x)=f(x),
又由f(1001+x)=f(1001-x)得f(2002-x)=f(x)
∴对任意的x都有f(x)=f(2002-x)=f(-x),f(x)是偶函数.
6、 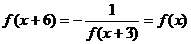 ,周期T=6, F(2007)=f(3)=6
,周期T=6, F(2007)=f(3)=6
[解答题]
5、f(x-1)=f(x)-f(x+1),∴f(x)=f(x+1)-f(x+2)=f(x+2)-f(x+3)-f(x+2)= -f(x+3)
∴f(x)= -f(x+3)=f(x+6) .周期是6;f(69)=f(3)=f(-3)= -f(-3+3)= -6
3、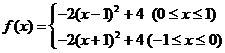 ; 4、8;
; 4、8;
2、D; f(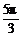 )=f(
)=f(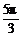 -2π)=f(-
-2π)=f(-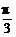 )=f(
)=f(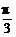 )=sin
)=sin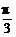 =
=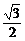 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com