
20.解 (1)∵函数F(x)=f(x)-3x2是奇函数,
∴F(-x)=-F(x),化简计算得b=3.
∵函数f(x)在x=-1处取极值,∴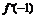 =0.
=0.
f(x)=-2x3+3x2+cx,
 =-6x2+6x+c
=-6x2+6x+c
∴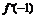 =-6-6+c=0,c=12.
=-6-6+c=0,c=12.
∴f(x)=-2x3+3x2+12x,
(2) =-6x2+6x+12=-6(x2-x-2).
=-6x2+6x+12=-6(x2-x-2).
令 =0,得x1=-1,x2=2,
=0,得x1=-1,x2=2,
|
x |
-3 |
(-3,-1) |
-1 |
(-1,2) |
2 |
(2,3) |
3 |
 |
|
- |
0 |
+ |
0 |
- |
|
|
f(x) |
45 |
↘ |
-7 |
↗ |
20 |
↘ |
9 |
∴函数f(x)在[-3,-1]和[2,3]上是减函数,
函数f(x)在[-1,2]上是增函数.
19.解 f(x)=x(x-1)(x-a)=x3-(a+1)x2+ax
∴ =3x2-2(a+1)x+a
=3x2-2(a+1)x+a
要使函数f(x)=x(x-1)(x-a)在(2,+∞)上是增函数,只需 =3x2-2(a+1)x+a在(2,+∞)上满足
=3x2-2(a+1)x+a在(2,+∞)上满足 ≥0即可. ∵
≥0即可. ∵ =3x2-2(a+1)x+a的对称轴是x=
=3x2-2(a+1)x+a的对称轴是x= ,
,
∴a的取值应满足: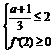 或
或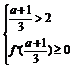
解得:a≤ .∴a的取值范围是a≤
.∴a的取值范围是a≤ .
.
18.解 命题p:由原式得f(x)=x3-ax2-4x+4a,
∴ =3x2-2ax-4,y′的图象为开口向上且过点(0,-4)的抛物线.
=3x2-2ax-4,y′的图象为开口向上且过点(0,-4)的抛物线.
由条件得 ≥0且
≥0且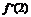 ≥0,
≥0,
即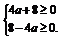 ∴-2≤a≤2.
∴-2≤a≤2.
命题q:
∵该不等式的解集为R,∴a<-1.
当p正确q不正确时,-1≤a≤2;
当p不正确q正确时,a<-2.
∴a的取值范围是(-∞,-2)∪[-1,2].
17.解 (1) =3x2-x+b,因f(x)在(-∞,+∞)上是增函数,则
=3x2-x+b,因f(x)在(-∞,+∞)上是增函数,则 ≥0.即3x2-x+b≥0,
≥0.即3x2-x+b≥0,
∴b≥x-3x2在(-∞,+∞)恒成立.设g(x)=x-3x2.
当x= 时,g(x)max=
时,g(x)max=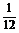 ,∴b≥
,∴b≥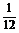 .
.
(2)由题意知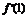 =0,即3-1+b=0,∴b=-2.
=0,即3-1+b=0,∴b=-2.
x∈[-1,2]时,f(x)<c2恒成立,只需f(x)在[-1,2]上的最大值小于c2即可.因 =3x2-x-2,令
=3x2-x-2,令 =0,得x=1或x=-
=0,得x=1或x=- .∵f(1)=-
.∵f(1)=- +c,
+c,
f(- f(2)=2+c.
f(2)=2+c.
∴f(x)max=f(2)=2+c,∴2+c<c2.解得c>2或c<-1,所以c的取值范围为(-∞,-1)∪(2,+∞).
16.答案 6
15.答案 [-1,0]和[2,+∞)
14.答案 ②③
13.答案 [-1,2]
12.答案?A?
11.答案?B?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com