
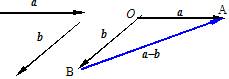
11.差向量的意义: 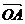 = a,
= a, 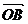 = b,
则
= b,
则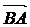 = a - b
= a - b
即a - b可以表示为从向量b的终点指向向量a的终点的向量
10.向量的减法向量a加上的b相反向量,叫做a与b的差即:a - b = a + (-b)
9.向量加法的结合律:( +
+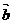 )
+
)
+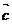 =
= +
(
+
(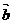 +
+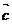 )
)
1向量的概念:既有大小又有方向的量叫向量,有二个要素:大小、方向
2向量的表示方法:①用有向线段表示;②用字母a、b等表示;
3零向量、单位向量概念:①长度为0的向量叫零向量,
②长度为1个单位长度的向量,叫单位向量
4平行向量定义:①方向相同或相反的非零向量叫平行向量;
②我们规定0与任一向量平行向量a、b、c平行,记作a∥b∥c
5相等向量定义:长度相等且方向相同的向量叫相等向量
6共线向量与平行向量关系:平行向量就是共线向量
7向量的加法:求两个向量和的运算,叫做向量的加法
向量加法的三角形法则和平行四边形法则
8. 向量加法的交换律:
向量加法的交换律: +
+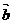 =
=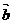 +
+
12.(15分)一辆汽车在十字路口等候绿灯,当绿灯亮时汽车以3 m/s2的加速度开始加速行驶,恰在这时一辆自行车以6 m/s的速度匀速驶来,从后边超过汽车.试求:汽车从路口启动后,在追上自行车之前经过多长时间两车相距最远?此时距离是多少?
解析:方法一:公式法
画出汽车和自行车的行程草图如图所示,当汽车的速度与自行车的速度相等时,两车之间的距离最大.
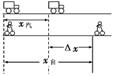 设经过时间t两车之间的距离最大.则有:v汽=at=v自
设经过时间t两车之间的距离最大.则有:v汽=at=v自
所以t== s=2 s
Δxm=x自-x汽=v自t-at2=6×2 m-×3×22 m=6 m
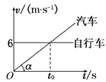 方法二:图象法
方法二:图象法
画出自行车和汽车的速度-时间图象如图所示,
自行车的位移x自等于其图线与时间轴围成的矩
形的面积,而汽车的位移x汽则等于其图线与时
间轴围成的三角形的面积.两车之间的距离则等于图中矩形的面积与三角形面积的差,不难看出,当t=t0时矩形与三角形的面积之差最大.
v-t图象的斜率表示物体的加速度
由a==3得t0=2 s
当t=2 s时两车的距离最大:Δxm=×2×6 m=6 m
方法三:二次函数极值法
设经过时间t汽车和自行车之间的距离为Δx,则
Δx=v自t-at2=6t-t2
当t=-=2 s时Δx有极大值
Δxm= m=6 m.
方法四:相对运动法
选自行车为参考系,则从开始运动到两车相距最远这段过程中,以汽车相对地面的运动方向为正方向,汽车相对此参考系的各个物理量分别为:v0=-6 m/s,a=3 m/s2,v=0
对汽车,由公式v=v0+at得

t== s=2 s
又知:v2-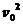 =2ax
=2ax
所以有x=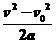 = m=-6 m
= m=-6 m
相距最远为6 m.
答案:2 s 6 m
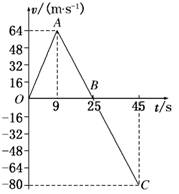
11.(15分)一宇宙空间探测器从某一星球表面垂直升空,
假设探测器的质量恒为1500 kg,发动机的推力为恒力,
宇宙探测器升空到某一高度时,发动机突然关闭,如图
10所示为其速度随时间的变化规律.图中9 s、25 s、45 s
三个时刻分别对应图象中的A、B、C三点.
(1)试定性分析探测器的运动情况;
(2)求探测器上升的最大高度. 图10
解析:(1)升空后探测器做初速度为零的匀加速直线运动.9 s末发动机关闭,此时速度最大,此后做匀减速运动,25 s末速度减为零,此时探测器离星球表面最高,再后探测器返回做自由落体运动,45 s末落地,速度大小为80 m/s.
(2)由(1)中分析知25 s末探测器距星球表面最高,最大高度hm=×25×64 m=800 m.
答案:(1)见解析 (2)800 m
10.处于平直轨道上的甲、乙两物体相距x,乙在甲前且两物体同时、同向开始运动,甲以初速度v、加速度a1做匀加速直线运动,乙做初速度为零、加速度为a2的匀加速直线运动,假设甲能从乙旁边通过,下述情况可能发生的是 ( )
A.a1=a2时,能相遇两次 B.a1>a2时,能相遇两次
C.a1<a2时,能相遇两次 D.a1<a2时,能相遇一次
解析:利用图象进行分析,如图所示,分别表示a1=a2时、a1>a2时、a1<a2时的速度图象.

对于A选项,甲的速度总是大于乙的速度,它们只能相遇一次,即甲追上乙车并超过乙;对于B选项,甲追上乙后,并超过乙,只能相遇一次;对于C选项,当甲、乙速度相等时,若是甲刚好追上乙,那么它们只能相遇一次,若是甲在速度未相等之前追上乙,以后乙的加速度比甲大,故其速度总会超过甲,乙会追上甲并超过甲,有可能相遇两次,若甲在速度与乙相等时还没有追上乙,则永远追不上乙,一次相遇的机会都没有.故正确答案为C、D.
 答案:CD
答案:CD
9.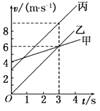 汽车的加速性能是反映汽车性能的重要指标.
汽车的加速性能是反映汽车性能的重要指标.
速度变化得越快,表明它的加速性能越好.如图9
所示为研究甲、乙、丙三辆汽车加速性能得到的
v-t图象,根据图象可以判定 ( )
A.甲车的加速性能最好 图9
B.乙比甲的加速性能好
C.丙比乙的加速性能好
D.乙、丙两车的加速性能相同
解析:图象的斜率表示加速度,加速度越大,加速性能越好.选项B、D正确.
答案:BD
8.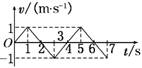 (2010·中山模拟)某质点的运动规律如图8所示,
(2010·中山模拟)某质点的运动规律如图8所示,
下列说法中正确的是 ( )
A.质点在第1 s末加速度的方向发生变化
B.质点在第2 s内和第3 s内加速度大小相等而方向相反 图8
C.质点在第3 s内速度越来越大
D.在前7 s内质点的位移为负值
解析:由v-t图象知,第1 s末的速度达到正向最大,之后速度减小,加速度为负向,故A正确;第2 s和第3 s内,尽管速度方向相反,但斜率相等,则加速度相等,B错;在第3 s内,速度的绝对值在增大,说明质点做反向加速运动,C正确;前7 s内图线所围的面积为正,则对应位移为正,D错.
答案:AC
7.(2008·广东高考)某人骑自行车在平直道路上行进,图7中的实线记录了自行车开始一段时间内的v-t图象.某同学为了简化计算,用虚线作近似处理,下列说法正确的是 ( )
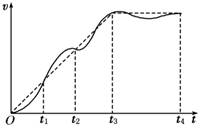
图7
A.在t1时刻,虚线反映的加速度比实际的大
B.在0-t1时间内,由虚线计算出的平均速度比实际的大
C.在t1-t2时间内,由虚线计算出的位移比实际的大
D.在t3-t4时间内,虚线反映的是匀速运动
解析:在v-t图象中斜率大小表示加速度的大小,图线与横轴围成的面积表示位移大小.故在t1时刻,虚线斜率小于实线切线的斜率,A错;在0-t1时间内,虚线与横轴围成的面积大于实线与横轴围成的面积,故由虚线计算出的平均速度比实际的大,B正确;在t1-t2时间内,虚线与横轴围成的面积比实线与横轴围成的面积小,故C错误;在t3-t4时间内,虚线平行于t轴,故虚线反映的是匀速运动,D正确.
答案:BD
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com