
5、 赠 别
杜牧
多情却似总无情,惟觉樽前笑不成。
蜡烛有心还惜别,替人垂泪到天明。
如何理解诗中蜡烛的形象及其作用?
4、 诉 衷 情
晏殊
芙蓉金菊斗馨香,天气欲重阳。远村秋色如画,红树间疏黄。
流水淡,碧天长,路茫茫。凭高目断,鸿雁来时,无限思量。
这首词写景极有特色,请简要分析。
2、 剑门道中遇微雨
陆游
衣上征尘杂酒痕,远游无处不消魂。
此身合是诗人未?细雨骑驴入剑门。
在诗的前两句中,由“酒痕”、“消魂”可以看出,诗人给我们展示了一个具有怎样情感特征的人物形象?
3 客 中 初 夏
司马光
四月清和雨乍晴,南山当户转分明。
更无柳絮因风起,惟有葵花向日倾。
散文创作有“形散而神不散”之说,请用这个说法分析《客中初夏》的“散”与“不散”。
1、 商 山 早 行
温庭筠
晨起动征铎,客行悲故乡。
鸡声茅店月,人迹板桥霜。
槲叶落山路,枳花明驿墙。
因思杜陵梦,凫雁满回塘。
“凫雁满回塘”表现了怎样的意境?联系首联解说作者这样写的意图。
1设e1、e2是同一平面内的两个向量,则有
Ae1、e2一定平行
Be1、e2的模相等
C同一平面内的任一向量a都有a=λe1+μe2(λ、μ∈R)
D若e1、e2不共线,则同一平面内的任一向量a都有a=λe1+ue2(λ、u∈R)
2已知矢量a=e1-2e2,b=2e1+e2,其中e1、e2不共线,则a+b与c=6e1-2e2的关系
A不共线 B共线 C相等 D无法确定
3已知向量e1、e2不共线,实数x、y满足(3x-4y)e1+(2x-3y)e2=6e1+3e2,则x-y的值等于 ?
A3? B-3 ?C0 ?D2
4若a、b不共线,且λa+μb=0(λ,μ∈R)则λ= ,μ=
5已知a、b不共线,且c=λ1a+λ2b(λ1,λ2∈R),若c与b共线,则λ1=
6已知λ1>0,λ2>0,e1、e2是一组基底,且a=λ1e1+λ2e2,则a与e1_____,
 例1 已知向量
例1 已知向量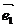 ,
, 求作向量-25
求作向量-25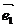 +3
+3
作法:(1)取点O,作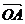 =-25
=-25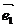
 =3
=3
(2)作 
 OACB,
OACB,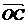 即为所求-25
即为所求-25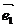 +3
+3
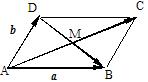
例2 如图 
 ABCD的两条对角线交于点M,且
ABCD的两条对角线交于点M,且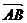 =
= ,
,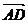 =
= ,用
,用 ,
, 表示
表示 ,
,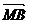 ,
,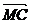 和
和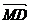
解:在 
 ABCD中 , ∵
ABCD中 , ∵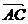 =
=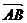 +
+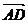 =
= +
+ ,
, =
=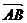 -
-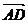 =
= -
-
 ∴
∴ =-
=-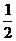
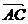 =-
=-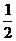 (
( +
+ )=-
)=-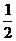
 -
-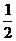
 ,
,
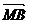 =
=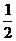
 =
=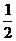 (
( -
- )=
)=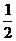
 -
-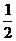

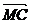 =
=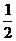
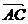 =
=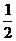
 +
+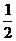

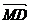 =-
=-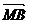 =-
=-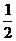
 =-
=-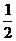
 +
+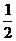

例3已知
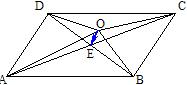
 ABCD的两条对角线AC与BD交于E,O是任意一点,
ABCD的两条对角线AC与BD交于E,O是任意一点,
 求证:
求证: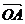 +
+ +
+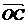 +
+ =4
=4
证明:∵E是对角线AC和BD的交点
∴ =
= =-
=-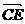 ,
,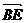 =
= =-
=-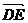
在△OAE中,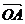 +
+ =
=
同理  +
+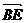 =
= ,
, 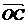 +
+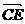 =
= ,
, +
+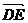 =
=
以上各式相加,得 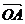 +
+ +
+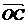 +
+ =4
=4
例4如图,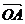 ,
, 不共线,
不共线, =t
=t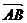 (tÎR)用
(tÎR)用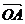 ,
, 表示
表示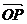
 解:∵
解:∵ =t
=t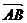
∴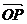 =
=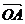 +
+ =
=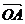 +
t
+
t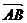
=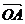 +
t(
+
t( -
-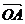 )=
)=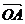 +
t
+
t -t
-t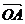 =(1-t)
=(1-t) 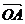 +
t
+
t
平面向量基本定理:如果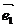 ,
, 是同一平面内的两个不共线向量,那么对于这一平面内的任一向量
是同一平面内的两个不共线向量,那么对于这一平面内的任一向量 ,有且只有一对实数λ1,λ2使
,有且只有一对实数λ1,λ2使 =λ1
=λ1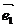 +λ2
+λ2
探究:(1)我们把不共线向量e1、e2叫做表示这一平面内所有向量的一组基底;
(2)基底不惟一,关键是不共线;
(3)由定理可将任一向量a在给出基底e1、e2的条件下进行分解;
(4)基底给定时,分解形式惟一λ1,λ2是被 ,
,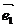 ,
, 唯一确定的数量
唯一确定的数量
14. 向量共线定理 向量 与非零向量
与非零向量 共线的充要条件是:有且只有一个非零实数λ,使
共线的充要条件是:有且只有一个非零实数λ,使 =λ
=λ
13.运算定律 结合律:λ(μ )=(λμ)
)=(λμ)
分配律:(λ+μ) =λ
=λ +μ
+μ λ(
λ( +
+ )=λ
)=λ +λ
+λ
12.实数与向量的积:实数λ与向量 的积是一个向量,记作:λ
的积是一个向量,记作:λ
(1)|λ |=|λ||
|=|λ|| |;(2)λ>0时λ
|;(2)λ>0时λ 与
与 方向相同;λ<0时λ
方向相同;λ<0时λ 与
与 方向相反;λ=0时λ
方向相反;λ=0时λ =
=
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com