
5.”双向储畜法”设每年还x元,第n年底还清,则所还款到第n年底的本利和为
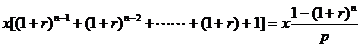
贷款A元到第n年底本利和为A(1+r)n.
由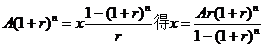
4.由a1·a2·…·ak=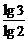 ·
· ·
·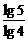 ·…·
·…·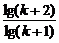 =
=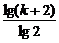 =log2(k+2)=2008,解之得k=22008-2.
=log2(k+2)=2008,解之得k=22008-2.
2.由题意列式(1-20%)n<5%,两边取对数得n>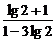 ≈13.4.故n≥14.
≈13.4.故n≥14.
1.一次砍伐后木材的存量为S(1+25%)-x;
二次砍伐后木材存量为[S(1+25%)-x](1+25%)-x.
由题意知(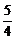 )2S-
)2S-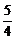 x-x=S(1+50%),解得x=
x-x=S(1+50%),解得x= .
.
6.5只猴子分一堆苹果,第一只猴子把苹果分成5堆,还多1个,把多的1个扔掉,取走其中的一堆,第二只猴子把剩下的苹果分成五堆,也多1个,把多的一个扔掉,也取走一堆,以后每只猴子都如此办理,则最后一只猴子所得苹果的最小值是 。
简答:1-3.CDC;
5.某企业在年度之初借款A元,从该年度末开始,每年度末偿还一定的金额,恰在n年间还清,年利率为r,试问每次需支付的金额是 元?
4.已知an=logn+1(n+2)(n∈N*),观察下列运算a1·a2=log23·log34=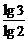 ·
· =2,
=2,
a1·a2·a3·a4·a5·a6=log23·log34·…·log67·log78=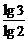 ·
· ·…·
·…· ·
·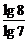 =3.
=3.
……
定义使a1·a2·a3·…·ak为整数的k(k∈N*)叫做企盼数.试确定当a1·a2·a3·…·ak=2008时,企盼数k=______________.
答案:22008-2
3.某工厂的产值月平均增长率为P,则年平均增长率为: ( )
A、12P
B、(1+P)11-1 C、(1+P)12-1 D、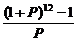
2.某纯净水制造厂在净化水过程中,每增加一次过滤可减少水中杂质20%,要使水中杂质减少到原来的5%以下,(lg2=0.301),则至少需过滤的次数为
A.5 B.10 C.13 D.14
1.某林场年初有森林木材存量S m3,木材以每年25%的增长率生长,而每年末要砍伐固定的木材量x m3,为实现经过两次砍伐后的木材的存量增加50%,则x的值是
A. B.
B.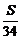 C.
C. D.
D.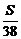
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com