
6.如图,它满足:(1)第n行首尾两数均为n;
(2)表中的递推关系类似杨辉三角,则第n行
(n≥2)第2个数是_______________.
简答.提示:1-4.DBDD; 4.第一次运运两根,所走路程a1=1100,以后每次比上次多走300米,共7次,路程总和S7=14000m;
5.假设一个球从某个高度掉到地上,再弹起的高度为前高度的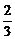 ,那么当一个球从6米高度落下,并让其自由弹跳直到停下,球总共的运动路程为 米。
,那么当一个球从6米高度落下,并让其自由弹跳直到停下,球总共的运动路程为 米。

4.从工地运送电线杆到500m以外的公路,沿公路一侧每隔50m埋栽一根电线杆,已知每次最多只能运3根,要完成运载20根电线杆的任务,最佳方案是使运输车运行( )
A.11700m B、14700m C、14500m D、14000m
3.某工厂去年产值为a,计划今后五年内每年比上一年产值增长10%,从今年起到第五年,这个工厂的总产值是 ( )
A、1.14a B、1.1(1.15-1)a C、10(1.15-1)a D、11(1.15-1)a
2.某工厂年产量第二年增长率为a,第三年增长率为b,则这两年平均增长率x满足
( )
A、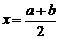 B、
B、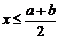 C、
C、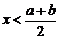 D、
D、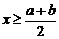
1.从2003年到2006年期间,甲每年6月1日都到银行存入m元一年定期储蓄,若年利率q保持不变,且每年到期的存款利息均自动转为新的一年定期,到2007年6月1日,甲去银行不再存款,而是将所有存款的本息作用全部取回,则取回的金额是:( )
A、m(1+q)4元 B、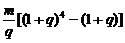 元 C、m(1+q)5元 D、
元 C、m(1+q)5元 D、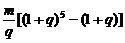 元
元
2.将实际问题转化为数列问题时应注意:
(1)分清是等差,还是等比数列问题;
(2)分清是求an还是求Sn,特别要准确地确定项数n.
(3)要要善于发现an与an-1的关系。
同步练习 3.7数列的应用
[选择题]
1.数列的应用题常见类型:产量增减、价格升降、求利率、增长率、细胞繁殖分期付款等,一般是等差、等比数列问题,解题关键是建立数列的模型;.
[例1]6.从2002年1月2日起,每年1月2日到银行存入一万元定期储蓄,若年利率为p,且保持不变,并约定每年到期存款均自动转为新一年的定期存款,到2008年1月2日不再存款,而是将所有存款及利息全部取回,求可取回的钱的总数(万元).
解:存款从后向前考虑
(1+p)+(1+p)2+…+(1+p)5
=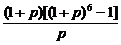
=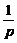 [(1+p)7-(1+p)].
[(1+p)7-(1+p)].
答: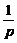 [(1+p)7-(1+p)]万元。
[(1+p)7-(1+p)]万元。
提炼方法:数列模型--等比数列的和,实质是复利、零存整取取问题。从最后一年存款向前算。
[例2]由于美伊战争的影响,据估计,伊拉克将产生60~100万难民,联合国难民署计划从4月1日起为伊难民运送食品.第一天运送1000 t,第二天运送1100 t,以后每天都比前一天多运送100 t,直到达到运送食品的最大量,然后再每天递减100 t,连续运送15天,总共运送21300 t,求在第几天达到运送食品的最大量.
剖析:本题实质上是一个等差数列的求通项和求和的问题.
解:设在第n天达到运送食品的最大量.
则前n天每天运送的食品量是首项为1000,公差为100的等差数列.
an=1000+(n-1)·100=100n+900.
其余每天运送的食品量是首项为100n+800,公差为-100的等差数列.
依题意,得
1000n+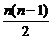 ×100+(100n+800)(15-n)+
×100+(100n+800)(15-n)+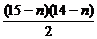 ×(-100)=21300(1≤n≤15).
×(-100)=21300(1≤n≤15).
整理化简得n2-31n+198=0.
解得n=9或22(不合题意,舍去).
答:在第9天达到运送食品的最大量.
温馨提示:对数列应用题要分清是求通项问题还是求和问题.
[例3]杭州某通讯设备厂为适应市场需求,提高效益,特投入98万元引进世界先进设备奔腾6号,并马上投入生产.第一年需要的各种费用是12万元,从第二年开始,所需费用会比上一年增加4万元,而每年因引入该设备可获得的年利润为50万元.
请你根据以上数据,解决下列问题:
(1)引进该设备多少年后,开始盈利?
(2)引进该设备若干年后,有两种处理方案:
第一种:年平均盈利达到最大值时,以26万元的价格卖出;
第二种:盈利总额达到最大值时,以8万元的价格卖出.
问哪种方案较为合算?并说明理由.
解:(1)设引进设备n年后开始盈利,盈利为y万元,则y=50n-(12n+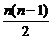 ×4)-98=-2n2+40n-98,由y>0,得10-
×4)-98=-2n2+40n-98,由y>0,得10-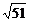 <n<10+
<n<10+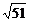 .
.
∵n∈N*,∴3≤n≤17,
即3年后开始盈利.
(2)方案一:年平均盈利为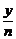 ,
,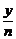 =-2n-
=-2n- +40≤-2
+40≤-2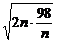 +40=12,
+40=12,
当且仅当2n= ,即n=7时,年平均利润最大,共盈利12×7+26=110万元.
,即n=7时,年平均利润最大,共盈利12×7+26=110万元.
方案二:盈利总额y=-2(n-10)2+102,n=10时,y取最大值102,
即经过10年盈利总额最大,
共计盈利102+8=110万元.
两种方案获利相等,但由于方案二时间长,所以采用方案一合算.
[例4] 2002年底某县的绿化面积占全县总面积的40%,从2003年开始,计划每年将非绿化面积的8%绿化,由于修路和盖房等用地,原有绿化面积的2%被非绿化.
(1)设该县的总面积为1,2002年底绿化面积为a1=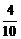 ,经过n年后绿化的面积为an+1,试用an表示an+1;
,经过n年后绿化的面积为an+1,试用an表示an+1;
(2)求数列{an}的第n+1项an+1;
(3)至少需要多少年的努力,才能使绿化率超过60%.(lg2=0.3010,lg3=0.4771)
剖析:当年的绿化面积等于上年被非绿化后剩余面积加上新绿化面积.
解:(1)设现有非绿化面积为b1,经过n年后非绿化面积为bn+1.
于是a1+b1=1,an+bn=1.
依题意,an+1是由两部分组成,一部分是原有的绿化面积an减去被非绿化部分 an后剩余的面积
an后剩余的面积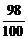 an,另一部分是新绿化的面积
an,另一部分是新绿化的面积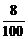 bn,于是
bn,于是
an+1=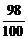 an+
an+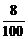 bn=
bn=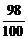 an+
an+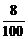 (1-an)
(1-an)
=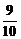 an+
an+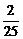 .
.
(2)an+1=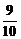 an+
an+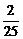 ,an+1-
,an+1-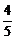 =
=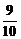 (an-
(an-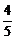 ).
).
数列{an-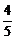 }是公比为
}是公比为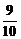 ,首项a1-
,首项a1-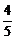 =
=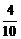 -
-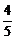 =-
=-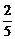 的等比数列.
的等比数列.
∴an+1=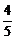 +(-
+(-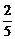 )(
)(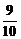 )n.
)n.
(3)an+1>60%,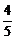 +(-
+(-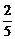 )(
)(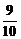 )n>
)n>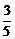 ,(
,(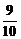 )n<
)n< ,n(lg9-1)<-lg2,n>
,n(lg9-1)<-lg2,n>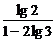 ≈6.5720.
≈6.5720.
至少需要7年,绿化率才能超过60%.
[研讨.欣赏]
(2004年春季北京,20)下表给出一个“等差数阵”:
|
4 |
7 |
( ) |
( ) |
( ) |
… |
a1j |
… |
|
7 |
12 |
( ) |
( ) |
( ) |
… |
a2j |
… |
|
( ) |
( ) |
( ) |
( ) |
( ) |
… |
a3j |
… |
|
( ) |
( ) |
( ) |
( ) |
( ) |
… |
a4j |
… |
|
… |
… |
… |
… |
… |
… |
… |
… |
|
ai1 |
ai2 |
ai3 |
ai4 |
ai5 |
… |
aij |
… |
|
… |
… |
… |
… |
… |
… |
… |
… |
其中每行、每列都是等差数列,aij表示位于第i行第j列的数.
(1)写出a45的值;
(2)写出aij的计算公式;
(3)证明:正整数N在该等差数阵中的充要条件是2N+1可以分解成两个不是1的正整数之积.
(1)解:a45=49.
(2)解:该等差数阵的第一行是首项为4,公差为3的等差数列:a1j=4+3(j-1),
第二行是首项为7,公差为5的等差数列:a2j=7+5(j-1),
……
第i行是首项为4+3(i-1),公差为2i+1的等差数列,
因此aij=4+3(i-1)+(2i+1)(j-1)=2ij+i+j=i(2j+1)+j.
(3)证明:必要性:若N在该等差数阵中,则存在正整数i、j使得N=i(2j+1)+j,
从而2N+1=2i(2j+1)+2j+1=(2i+1)(2j+1),
即正整数2N+1可以分解成两个不是1的正整数之积.
充分性:若2N+1可以分解成两个不是1的正整数之积,由于2N+1是奇数,则它必为两个不是1的奇数之积,即存在正整数k、l,使得2N+1=(2k+1)(2l+1),
从而N=k(2l+1)+l=akl,
可见N在该等差数阵中.
综上所述,正整数N在该等差数阵中的充要条件是2N+1可以分解成两个不是1的正整数之积.
6.设第n只猴得an只苹果,则
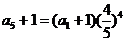 ,是整数则(a1+1)=54时,
,是整数则(a1+1)=54时,
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com