
9.解不等式:(1)  ≤1 (2)(x2-1)(x2-4x-5)>0
≤1 (2)(x2-1)(x2-4x-5)>0
(3)  (4)
(4) 
8.已知不等式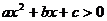 的解集为(
的解集为( ,则不等式
,则不等式 的解集为
的解集为
7. (2006年江苏 16)不等式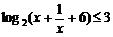 的解集为
.
的解集为
.
6.已知关于x的方程si 有实数解,则a的范围是
。
有实数解,则a的范围是
。
5.方程 的两根都是负数,则
的两根都是负数,则 的取值范围是
的取值范围是
4.(2006年山东
理 3)设f(x)=
 则不等式f(x)>2的解集为( )
则不等式f(x)>2的解集为( )
(A)(1,2) (3,+∞)
(B)(
(3,+∞)
(B)( ,+∞)
,+∞)
(C)(1,2) (
( ,+∞) (D)(1,2)
,+∞) (D)(1,2)
3.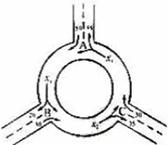 (2006年北京 理 8)下图为某三岔路口交通环岛的简化模型,在某高峰时段,单位时间进出路口 A、B、 C 的机动车辆数如图所示,图中
(2006年北京 理 8)下图为某三岔路口交通环岛的简化模型,在某高峰时段,单位时间进出路口 A、B、 C 的机动车辆数如图所示,图中
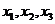 分别表示该时段单位时间通过路段
分别表示该时段单位时间通过路段 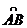 ,
,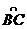 ,
,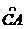 的机动车辆数(假设:单位时间内,在上述路段中,同一路段上驶入与驶出的车辆数相等),则
( )
的机动车辆数(假设:单位时间内,在上述路段中,同一路段上驶入与驶出的车辆数相等),则
( )
(A) 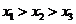 (B)
(B)
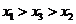
(C)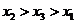 (D)
(D)
2.关于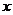 的不等式
的不等式 对
对 恒成立,则实数
恒成立,则实数 ( )
( )
A.(1,3) B.(-∞,1)∪(3,+∞) C.(-1,3) D.(-3,-1)
1.设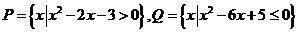 ,则
,则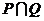 =-------( )
=-------( )
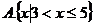
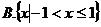


7.不等式(x2+px+q)<0的解集是{x︱1<x<2},则不等式(x2+px+q)(x2-5x-6)>0的解集是 .
[典型例题]
例1.解下列不等式:
(1)x2-7x+12>0; (2)-x2-2x+3≥0; (3)x2-2x+1<0; ( 4)x2-2x+2>0;
(5)x<x2-x-1<x2; (6)(x-2)(x2+x-2)(x2-x+3)≤0
(7) ≥3 (8)x2-(a+
≥3 (8)x2-(a+ )x+1<0(a>0)
)x+1<0(a>0)
例2. 关于x的不等式组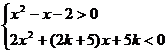 的整数解的集合为{-2},求实数
的整数解的集合为{-2},求实数 的取值范围.
的取值范围.
例3.若不等式 对一切
对一切 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
例4.已知关于x的防方程 分别根据下列条件求a的范围
分别根据下列条件求a的范围
(1)两根均为正;(2)两根均为负;(3)一根正一根负;(4)至少有一根为正;
(5)一根大于1,一根小于1;(6)两根均大于1;(7)两根均小于1;
(8)两根在 之内;(9)一根大于1,一根小于
之内;(9)一根大于1,一根小于 ;(10)一根在
;(10)一根在 内,一根在
内,一根在 内。
内。
例6. 汽车在行驶中,由于惯性的作用,刹车后还要继续向前滑行一段距离才能停住,我们称这段距离为刹车距离,刹车距离是分析事故的一个重要的因素;
在一个限速为40km/h的弯道上,甲、乙两辆汽车相向而行,发现情况不对,同时刹车,但是还是向碰了,事后现场勘查测得甲车的刹车距离略超过12m,乙车的刹车距离略超过10m,又知甲乙两车的刹车距离s(m)和车速x(km/h)之间分别有如下的关系:
S甲=0.1x+0.01x2, S乙=0.05x+0.005x2,问:甲乙有无超速现象?
[巩固练习]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com