
8.已知某人每天早晨乘坐的某一班次公共汽车的准时到站率为60%,则他在3天乘车中,此班次公共汽车至少有2天准时到站的概率为 ( )
A. B.
B.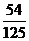 C.
C. D.
D.
7.在圆周上有10个等分,以这些点为顶点,每3个点可以构成一个三角形,如果随机选择了3个点,刚好构成直角三角形的概率是( )
A.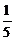 B.
B.
 C.
C.
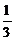 D.
D. 
6.(汉沽一中2008~2009届月考文9).面积为S的△ABC,D是BC的中点,向△ABC内部投一点,那么点落在△ABD内的概率为 ( )
A. B.
B.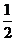 C.
C. D.
D.
5.(汉沽一中2008~2009届月考文9).面积为S的△ABC,D是BC的中点,向△ABC内部投一点,那么点落在△ABD内的概率为 ( )
A. B.
B.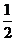 C.
C. D.
D.
3.设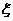 是离散型随机变量,
是离散型随机变量, ,
,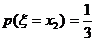 ,且
,且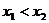 ,现已知:
,现已知: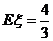 ,
,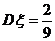 ,则
,则 的值为( )
的值为( )
(A)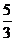 (B)
(B) (C) 3 (D)
(C) 3 (D)  4.福娃是北京2008年第29届奥运会吉祥物,每组福娃都由“贝贝”、“晶晶”、“欢欢”、“迎迎”和“妮妮”这五个福娃组成.甲、乙两位好友分别从同一组福娃中各随机选择一个福娃留作纪念,按先甲选再乙选的顺序不放回地选择,则在这两位好友所选择的福娃中,“贝贝”和“晶晶”恰好只有一个被选中的概率为( )
4.福娃是北京2008年第29届奥运会吉祥物,每组福娃都由“贝贝”、“晶晶”、“欢欢”、“迎迎”和“妮妮”这五个福娃组成.甲、乙两位好友分别从同一组福娃中各随机选择一个福娃留作纪念,按先甲选再乙选的顺序不放回地选择,则在这两位好友所选择的福娃中,“贝贝”和“晶晶”恰好只有一个被选中的概率为( )
A.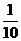 B.
B. C.
C.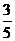 D.
D.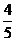
2.一射手对同一目标独立地射击四次,已知至少命中一次的概率为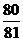 ,则此射手每次射击命中的概率为( )
,则此射手每次射击命中的概率为( )
A. B. C. D.
1.已知非空集合A、B满足A B,给出以下四个命题:
B,给出以下四个命题:
①若任取x∈A,则x∈B是必然事件 ②若x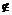 A,则x∈B是不可能事件
A,则x∈B是不可能事件
③若任取x∈B,则x∈A是随机事件 ④若x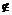 B,则x
B,则x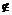 A是必然事件
A是必然事件
其中正确的个数是( )
A、1 B、2 C、3 D、4
22、已知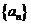 是公差为
是公差为 的等差数列,它的前
的等差数列,它的前 项和为
项和为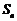 ,
,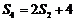 ,
,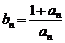 .
.
(1)求公差 的值;
的值;
(2)若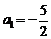 ,求数列
,求数列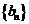 中的最大项和最小项的值;
中的最大项和最小项的值;
(3)若对任意的 ,都有
,都有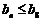 成立,求
成立,求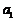 的取值范围.
的取值范围.
21、已知直线 与圆
与圆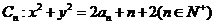 交于不同点An、Bn,其中数列
交于不同点An、Bn,其中数列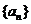 满足:
满足: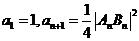 .
.
(1)求数列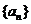 的通项公式;
的通项公式;
(2)设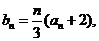 求数列
求数列 的前n项和
的前n项和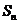 .
.
20、已知数列 中,
中,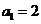 ,
,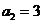 ,其前
,其前 项和
项和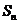 满足
满足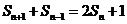 (
( ,
,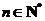 ).(1)求数列
).(1)求数列 的通项公式;
的通项公式;
(2)设 为非零整数,
为非零整数,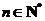 ),试确定
),试确定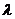 的值,使得对任意
的值,使得对任意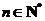 ,都有
,都有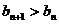 成立.
成立.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com