
21.(本题满分12分)已知数列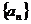 ,其中
,其中 ,且
,且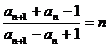 .
.
(1)求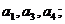
(2)求数列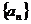 的通项公式;
的通项公式;
(3)设数列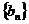 为等差数列,其中
为等差数列,其中 且c为不等于零的常数,若
且c为不等于零的常数,若
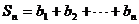 .求
.求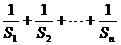 .
.
20.(本题满分12分)某城市有甲、乙、丙3个旅游景点,一位客人游览这三个景点的概率分别是0.4,0.5,0.6,且客人是否游览哪个景点互不影响,设ξ表示客人离开该城市时游览的景点数与没有游览的景点数之差的绝对值.
(Ⅰ)求ξ的分布列及数学期望;
(Ⅱ)记“函数f(x)=x2-3 ξx+1在区间[2,+∞ 上单调递增”为事件A,求事件A的概率.
上单调递增”为事件A,求事件A的概率.
19.(本题满分12分)已知函数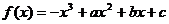 图像上的点
图像上的点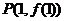 处的切线方程为
处的切线方程为 .
.
(1)若函数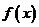 在
在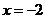 时有极值,求
时有极值,求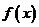 的表达式;
的表达式;
(2)函数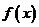 在区间
在区间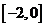 上单调递增,求实数
上单调递增,求实数 的取值范围.
的取值范围.
17(本题满分10分)已知圆 和圆
和圆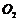 的极坐标方程分别为
的极坐标方程分别为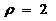 ,
,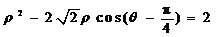 .
.
(1)把圆 和圆
和圆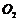 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)求经过两圆交点的直线的极坐标方程.
18.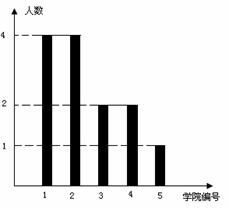 (本题满分12分)2010年上海世博会举办时间为2010年5月1日--10月31日.此次世博会福建馆招募了60名志愿者,某高校有13人入选,其中5人为中英文讲解员,8人为迎宾礼仪,它们来自该校的5所学院(这5所学院编号为1、2、3、4、5号),人员分布如图所示. 若从这13名入选者中随机抽出3人.
(本题满分12分)2010年上海世博会举办时间为2010年5月1日--10月31日.此次世博会福建馆招募了60名志愿者,某高校有13人入选,其中5人为中英文讲解员,8人为迎宾礼仪,它们来自该校的5所学院(这5所学院编号为1、2、3、4、5号),人员分布如图所示. 若从这13名入选者中随机抽出3人.
(Ⅰ)求这3人所在学院的编号正好成等比数列
的概率;
(Ⅱ)求这3人中中英文讲解员人数的分布列
及数学期望.
16.从装有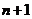 个球(其中
个球(其中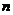 个白球,1个黑球)的口袋中取出
个白球,1个黑球)的口袋中取出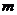 个球
个球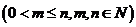 ,共有
,共有 种取法。在这
种取法。在这 种取法中,可以分成两类:一类是取出的
种取法中,可以分成两类:一类是取出的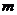 个球全部为白球,另一类是含有一个黑球,共有
个球全部为白球,另一类是含有一个黑球,共有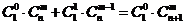 ,即有等式:
,即有等式: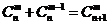 成立.试根据上述思想化简下列式子
成立.试根据上述思想化简下列式子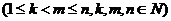 :
:
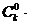
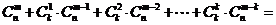 .
.
15.用4种不同的颜色涂入图中编号为1、2、3、4的正方形,要求每个正方形只涂一种颜色,且有公共边的两个正方形颜色不同,则不同的涂法有__________种.
14.直线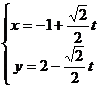 (
(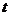 为参数)上到点A(
为参数)上到点A(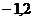 )的距离为
)的距离为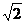 ,且在点A上方的点的坐标是
_______.
,且在点A上方的点的坐标是
_______.
|
1 |
2 |
|
3 |
4 |
13.某单位为了了解用电量y度与气温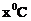 之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表:
之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表:
|
气温(0C) |
18 |
13 |
10 |
-1 |
|
用电量(度) |
24 |
34 |
38 |
64 |
由表中数据得线性回归方程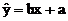 中
中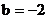 ,预测当气温为
,预测当气温为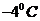 时,用电量的度数约为________.
时,用电量的度数约为________.
12. 内有任意三点不共线的2009个点.把这2009个点和三角形的三个顶点连线组成互不重叠的小三角形,则一共可组成( )个小三角形.
内有任意三点不共线的2009个点.把这2009个点和三角形的三个顶点连线组成互不重叠的小三角形,则一共可组成( )个小三角形.
A.4016 B.4017 C.4018 D.4019
11.将一骰子向上抛掷两次,所得点数分别为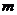 和
和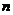 ,则函数
,则函数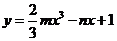 在
在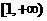 上为增函数的概率是( ).
上为增函数的概率是( ).
A.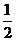 B.
B.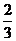 C.
C. D.
D.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com