
11.如图,矩形ABCD中,AB=5,BC=2,点B在直线L上,点A到
直线L的距离AE=3,则点C到直线L的距离CF为 .
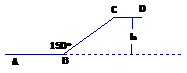 12.如图,是某商场一楼与二楼之间的手扶电梯示意图,
12.如图,是某商场一楼与二楼之间的手扶电梯示意图,
其中AB,CD分别表示一楼、二楼地面的水平线,∠ABC=150°,
 BC的长时8m,则乘电梯从点B到点C上升的高度h为
米.
BC的长时8m,则乘电梯从点B到点C上升的高度h为
米.
 9.计算:
9.计算: =
.
=
.
10.一次函数y=3x+b的图象过点(1,2),则b的值为 .
6.如图,平面直角坐标系中,在边长为1的正方形ABCD的边上
有一动点P沿A→B→C→D→A运动一周,则P点的纵坐标y与
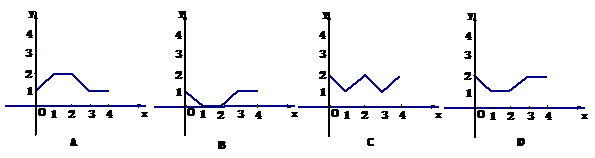 点P走过的路程s之间的函数关系用图象表示大致是( )
点P走过的路程s之间的函数关系用图象表示大致是( )
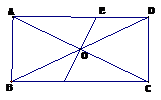 7.矩形ABCD中,AB=3,BC=5,过对角线交点作OE⊥AC交
7.矩形ABCD中,AB=3,BC=5,过对角线交点作OE⊥AC交
AD于点E,则AE的长是( )
A. 1.6 B. 2.5 C. 3 D. 3.4
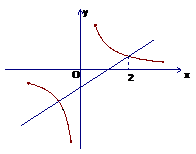
 8.如图,在平面直角坐标系中,OB在x轴上,∠ABO=90º,点A的坐标是(1,2)。将△AOB绕点A逆时针旋转90º,点O的对应点C恰好落在双曲线
8.如图,在平面直角坐标系中,OB在x轴上,∠ABO=90º,点A的坐标是(1,2)。将△AOB绕点A逆时针旋转90º,点O的对应点C恰好落在双曲线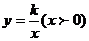 上,则K的值为( )
上,则K的值为( )
A.2 B.3
C.4 D.6
4.在Rt△ABC中,∠ACB=90°,BC=1,AB=2,则下列结论正确的是( )
A.sinA=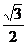 B.tanA=
B.tanA=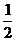 C.cosB=
C.cosB=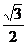 D.tanB=
D.tanB=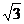
 5. 两个等腰直角三角形斜边的比是1:2,那么它们对应的面积比是( )
5. 两个等腰直角三角形斜边的比是1:2,那么它们对应的面积比是( )
A.1: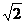 B.1:2 C.1:4
D.1:1
B.1:2 C.1:4
D.1:1
3.点P(m+2,m)在x轴上,则P点的坐标是( )
A.(-2,0) B.(2,0) C.(0,-2) D.(0,2)
2.长度单位1纳米=10-9米,目前发现一种新型病毒直径为25100纳米,用科学记数法表示该病毒直径是( )
A.25.1×10-6米 B.0.251×10-4米 C.2.51×105米 D.2.51×10-5米
1.使代数式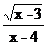 有意义的x的取值范围是( )
有意义的x的取值范围是( )
A.x>3 B.x≥3 C.x>4 D.x≥3且x≠4
答案:1.(1)若一个整数的末位是0,则它可以被5整除;
(2)若一个点在线段的垂直平分线上,则它与这条线段两个端点的距离相等;
(3)若一个式子是等式,则它的两边都乘以同一个数,所得结果仍是等式;
(4)若一条直线到圆心的距离不等于半径,则它不是圆的切线.
2.(1)可以被5 整除的整数,末位是0;
(2)不在线段的垂直平分线上的点与这条线段两个端点的距离不相等;
(3)若式子两边都乘以同一个数所得结果不是等式,则这个式子不是等式;
(4)若一条直线是圆的切线,则它到圆心的距离等于半径.
补充题:
写出命题“若 xy= 0 则 x = 0或 y = 0”的逆命题、否命题、逆否命题
解:逆命题:若 x = 0或 y = 0 则 xy = 0
否命题:若 xy ¹ 0 则 x ¹ 0且 y ¹ 0
逆否命题:若 x ¹ 0且 y ¹ 0 则 xy¹0.
注意: 1°为什么称“互为”逆命题(否命题,逆否命题)
2°要重视对命题的剖析:条件、结论
例1.(课本第P页30例1)把下列命题改写成“若p则q”的形式,并写出它们的逆命题、否命题与逆否命题:(学生回答,教师整理补充)
(1) 负数的平方是正数;(2)正方形的四条边相等.
分析:关键是找出原命题的条件p和结论q.
解:(1)原命题可以写成:若一个数是负数,则它的平方是正数;
逆命题:若一个数的平方是正数,则它是负数;
否命题:若一个数不是负数,则它的平方不是正数;
逆否命题:若一个数的平方不是正数,则它不是负数.
另解:原命题可写成:若一个数是负数的平方,则这个数是正数;
逆命题:若一个数是正数,则它是负数的平方;
否命题:若一个数不是负数的平方,则这个数不是正数;
逆否命题:若一个数不是正数,则它不是负数的平方.
(2) 原命题可写成:若一个四边形是正方形,则它的四条边相等;
逆命题:若一个四边形的四条边相等,则它是正方形;
否命题:若一个四边形不是正方形,则它的四条边不相等;
逆否命题:若一个四边形的四条边不相等,则它不是正方形.
例2.设原命题是“当c>0时,若a>b,则ac>bc”,写出它的逆命题、否命题与逆否命题,并判断它们的真假
注意:①“若p则q”形式的命题,也是一种复合命题,其中的p与q,可以是命题,也可以是开语句,例如,命题“若 =0,则x,y全为0”,其中的p与q,就是开语句.
=0,则x,y全为0”,其中的p与q,就是开语句.
②关键是找出原命题的条件(p)、结论(q),然后适当改写成更明显的形式
3.四中命题的形式
若p为原命题条件,q为原命题结论(学生回答,教师整理补充)
则:原命题:若 p 则 q
逆命题:若 p 则 q
否命题:若 Øp 则 Øq
逆否命题:若 Øq 则 Øp
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com