
7. (2010广东广州,7,3分)长方体的主视图与俯视图如图所示,则这个长方体的体积是( )
A.52 B.32 C.24 D.9
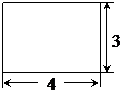

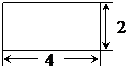

主视图 俯视图
[分析]由主视图可知,这个长方体的长和高分别为4和3,由俯视图可知,这个长方体的长和宽分别为4和2,因此这个长方体的长、宽、高分别为4、2、3,因此这个长方体的体积为4×2×3=24平方单位.
[答案]C
[涉及知识点]三视图
[点评]三视图问题一直是中考考查的高频考点,一般题目难度中等偏下,本题是由两种视图来推测整个正方体的特征,这种类型问题在中考试卷中经常出现,本题所用的知识是:主视图主要反映物体的长和高,左视图主要反映物体的宽和高,俯视图主要反映物体的长和宽.
[推荐指数]★★★★
6. (2010广东广州,6,3分)从图2的四张印有汽车品牌标志图案的卡片中任取一张,取出印有汽车品牌标志的图案是中心对称称图形的卡片的概率是( )




图2
A.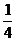 B.
B.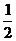 C.
C.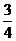 D.1
D.1
[分析]在这四个图片中只有第三幅图片是中心对称图形,因此是中心对称称图形的卡片的概率是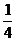 .
.
[答案]A
[涉及知识点]中心对称图形 概率
[点评]本题将两个简易的知识点,中心对称图形和概率组合在一起,是一个简单的综合问题,其中涉及的中心对称图形是指这个图形绕着对称中心旋转180°后仍然能和这个图形重合的图形,简易概率求法公式:P(A)=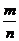 ,其中0≤P(A)≤1.
,其中0≤P(A)≤1.
[推荐指数]★★★★
5. (2010广东广州,5,3分)不等式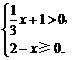 的解集是( )
的解集是( )
A.-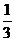 <x≤2
B.-3<x≤2 C.x≥2 D.x<-3
<x≤2
B.-3<x≤2 C.x≥2 D.x<-3
[分析]解不等式①,得:x>-3;解不等式②,得:x≤2,所以不等式组的解集为-3<x<2.
[答案]B
[涉及知识点]解不等式组
[点评]解不等式组是考查学生的基本计算能力,求不等式组解集的时候,可先分别求出组成不等式组的各个不等式的解集,然后借助数轴或口诀求出所有解集的公共部分.
[推荐指数]★★★
4. (2010广东广州,4,3分)在△ABC中,D、E分别是边AB、AC的中点,若BC=5,则DE的长是( )
A.2.5 B.5 C.10 D.15
[分析]由D、E分别是边AB、AC的中点可知,DE是△ABC的中位线,根据中位线定理可知,DE=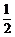 BC=2.5.
BC=2.5.
[答案]A
[涉及知识点]中位线
[点评]本题考查了中位线的性质,三角形的中位线是指连接三角形两边中点的线段,中位线的特征是平行于第三边且等于第三边的一半.
[推荐指数]★★
3. (2010广东广州,3,3分)下列运算正确的是( )
A.-3(x-1)=-3x-1 B.-3(x-1)=-3x+1
C.-3(x-1)=-3x-3 D.-3(x-1)=-3x+3
[分析]去括号时,要按照去括号法则,将括号前的-3与括号内每一项分别相乘,尤其需要注意,-3与-1相乘时,应该是+3而不是减3.
[答案]D
[涉及知识点]去括号
[点评]本题属于基础题,主要考查去括号法则,理论依据是乘法分配律,容易出错的地方有两处,一是-3只与x相乘,忘记乘以-1;二是-3与-1相乘时,忘记变符号.本题直指去括号法则,没有任何其它干扰,掌握了去括号法则就能得分,不掌握就不能得分,信度相当好.
[推荐指数]★★
2. (2010广东广州,2,3分)将图1所示的直角梯形绕直线l旋转一周,得到的立体图开是( )

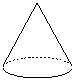
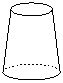
A. B. C. D. 图1
[分析]图1是一个直角题型,上底短,下底长,绕对称轴旋转后上底形成的圆小于下底形成的圆,因此得到的立体图形应该是一个圆台.
[答案]C
[涉及知识点]面动成体
[点评]本题属于基础题,主要考查学生是否具有基本的识图能力,以及对点线面体之间关系的理解,考查知识点单一,有利于提高本题的信度.
[推荐指数]★
1. (2010广东广州,1,3分)如果+10%表示“增加10%”,那么“减少8%”可以记作( )
A.-18% B.-8% C.+2% D.+8%
[分析]正数和负数可以表示一对相反意义的量,在本题中“增加”和“减小”就是一对相反意义的量,既然增加用正数表示,那么减少就用负数来表示,后面的百分比的值不变.
[答案]B
[涉及知识点]负数的意义
[点评]本题属于基础题,主要考查学生对概念的掌握是否全面,考查知识点单一,有利于提高本题的信度.
[推荐指数]★
22.如图(1),(2)所示,矩形ABCD的边长AB=6,BC=4,点F在DC上,DF=2。动点M、N分别
从点D、B同时出发,沿射线DA、线段BA向点A的方向运动(点M可运动到DA的延长线上),
当动点N运动到点A时,M、N两点同时停止运动。连接FM、FN,当F、N、M不在同一直线时,
可得△FMN,过△FMN三边的中点作△PQW。设动点M、N的速度都是1个单位/秒,M、N运动的
时间为x秒。试解答下列问题:
(1)说明△FMN∽△QWP;
(2)设0≤x≤4(即M从D到A运动的时间段)。试问x为何值时,△PQW为直角三角形?
当x在何范围时,△PQW不为直角三角形?
 (3)问当x为何值时,线段MN最短?求此时MN的值。
(3)问当x为何值时,线段MN最短?求此时MN的值。

2010年广东省中山市初中毕业生学业考试
20.已知两个全等的直角三角形纸片ABC、DEF,如图(1)放置,点B、D重合,点F在BC上,AB与EF交于点G。∠C=∠EFB=90º,∠E=∠ABC=30º,AB=DE=4。
(1)求证:△EGB是等腰三角形;
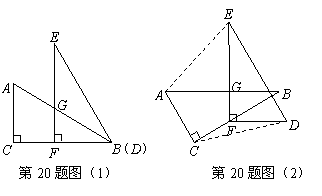 (2)若纸片DEF不动,问△ABC绕点F逆时针旋转最小_____度时,四边形ACDE成为以ED为底的梯形(如图(2)),求此梯形的高。
(2)若纸片DEF不动,问△ABC绕点F逆时针旋转最小_____度时,四边形ACDE成为以ED为底的梯形(如图(2)),求此梯形的高。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com