
2.下列运算正确的是( )
 A.
A. 3
B.
3
B.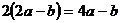
C. D.
D.
1.(2010·汕头)-3的相反数是( )
A.3 B. C.-3 D.
C.-3 D.
25.(2010广东广州,25,14分)如图所示,四边形OABC是矩形,点A、C的坐标分别为(3,0),(0,1),点D是线段BC上的动点(与端点B、C不重合),过点D作直线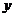 =-
=- +
+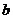 交折线OAB于点E.
交折线OAB于点E.
(1)记△ODE的面积为S,求S与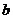 的函数关系式;
的函数关系式;
(2)当点E在线段OA上时,若矩形OABC关于直线DE的对称图形为四边形OA1B1C1,试探究OA1B1C1与矩形OABC的重叠部分的面积是否发生变化,若不变,求出该重叠部分的面积;若改变,请说明理由.


[分析](1)要表示出△ODE的面积,要分两种情况讨论,①如果点E在OA边上,只需求出这个三角形的底边OE长(E点横坐标)和高(D点纵坐标),代入三角形面积公式即可;②如果点E在AB边上,这时△ODE的面积可用长方形OABC的面积减去△OCD、△OAE、△BDE的面积;
(2)重叠部分是一个平行四边形,由于这个平行四边形上下边上的高不变,因此决定重叠部分面积是否变化的因素就是看这个平行四边形落在OA边上的线段长度是否变化.
[答案](1)由题意得B(3,1).
若直线经过点A(3,0)时,则b=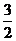
若直线经过点B(3,1)时,则b=
若直线经过点C(0,1)时,则b=1
①若直线与折线OAB的交点在OA上时,即1<b≤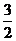 ,如图25-a,
,如图25-a,


此时E(2b,0)
∴S=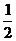 OE·CO=
OE·CO=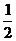 ×2b×1=b
×2b×1=b
②若直线与折线OAB的交点在BA上时,即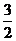 <b<
<b< ,如图2
,如图2


此时E(3, ),D(2b-2,1)
),D(2b-2,1)
∴S=S矩-(S△OCD+S△OAE +S△DBE )
= 3-[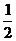 (2b-1)×1+
(2b-1)×1+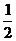 ×(5-2b)·(
×(5-2b)·( )+
)+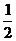 ×3(
×3( )]=
)]=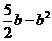
∴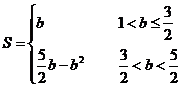
(2)如图3,设O1A1与CB相交于点M,OA与C1B1相交于点N,则矩形OA1B1C1与矩形OABC的重叠部分的面积即为四边形DNEM的面积。
本题答案由无锡市天一实验学校金杨建老师草制!
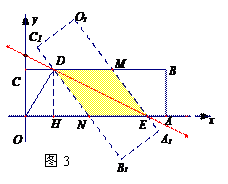

由题意知,DM∥NE,DN∥ME,∴四边形DNEM为平行四边形
根据轴对称知,∠MED=∠NED
又∠MDE=∠NED,∴∠MED=∠MDE,∴MD=ME,∴平行四边形DNEM为菱形.
过点D作DH⊥OA,垂足为H,
由题易知,tan∠DEN=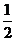 ,DH=1,∴HE=2,
,DH=1,∴HE=2,
设菱形DNEM 的边长为a,
则在Rt△DHM中,由勾股定理知: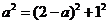 ,∴
,∴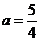
∴S四边形DNEM=NE·DH=
∴矩形OA1B1C1与矩形OABC的重叠部分的面积不发生变化,面积始终为 .
.
[涉及知识点]轴对称 四边形 勾股定理
[点评]本题是一个动态图形中的面积是否变化的问题,看一个图形的面积是否变化,关键是看决定这个面积的几个量是否变化,本题题型新颖是个不可多得的好题,有利于培养学生的思维能力,但难度较大,具有明显的区分度.
[推荐指数]★★★★★
24.(2010广东广州,24,14分)如图,⊙O的半径为1,点P是⊙O上一点,弦AB垂直平分线段OP,点D是 上任一点(与端点A、B不重合),DE⊥AB于点E,以点D为圆心、DE长为半径作⊙D,分别过点A、B作⊙D的切线,两条切线相交于点C.
上任一点(与端点A、B不重合),DE⊥AB于点E,以点D为圆心、DE长为半径作⊙D,分别过点A、B作⊙D的切线,两条切线相交于点C.
(1)求弦AB的长;
(2)判断∠ACB是否为定值,若是,求出∠ACB的大小;否则,请说明理由;
(3)记△ABC的面积为S,若 =4
=4 ,求△ABC的周长.
,求△ABC的周长.


[分析](1)连接OA,OP与AB的交点为F,则△OAF为直角三角形,且OA=1,OF=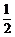 ,借助勾股定理可求得AF的长;
,借助勾股定理可求得AF的长;
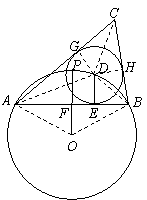

(2)要判断∠ACB是否为定值,只需判定∠CAB+∠ABC的值是否是定值,由于⊙D是△ABC的内切圆,所以AD和BD分别为∠CAB和∠ABC的角平分线,因此只要∠DAE+∠DBA是定值,那么CAB+∠ABC就是定值,而∠DAE+∠DBA等于弧AB所对的圆周角,这个值等于∠AOB值的一半;
(3)由题可知 =
=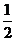 DE (AB+AC+BC),又因为
DE (AB+AC+BC),又因为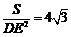 ,所以
,所以 ,所以AB+AC+BC=
,所以AB+AC+BC=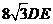 ,由于DH=DG=DE,所以在Rt△CDH中,CH=
,由于DH=DG=DE,所以在Rt△CDH中,CH= DH=
DH= DE,同理可得CG=
DE,同理可得CG= DE,又由于AG=AE,BE=BH,所以AB+AC+BC=CG+CH+AG+AB+BH=
DE,又由于AG=AE,BE=BH,所以AB+AC+BC=CG+CH+AG+AB+BH= DE+
DE+ ,可得
,可得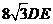 =
= DE+
DE+ ,解得:DE=
,解得:DE= ,代入AB+AC+BC=
,代入AB+AC+BC= ,即可求得周长为
,即可求得周长为 .
.
[答案]解:(1)连接OA,取OP与AB的交点为F,则有OA=1.


∵弦AB垂直平分线段OP,∴OF=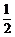 OP=
OP=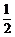 ,AF=BF.
,AF=BF.
在Rt△OAF中,∵AF= =
=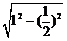 =
=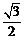 ,∴AB=2AF=
,∴AB=2AF= .
.
(2)∠ACB是定值.
理由:由(1)易知,∠AOB=120°,
因为点D为△ABC的内心,所以,连结AD、BD,则∠CAB=2∠DAE,∠CBA=2∠DBA,
因为∠DAE+∠DBA=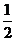 ∠AOB=60°,所以∠CAB+∠CBA=120°,所以∠ACB=60°;
∠AOB=60°,所以∠CAB+∠CBA=120°,所以∠ACB=60°;
(3)记△ABC的周长为l,取AC,BC与⊙D的切点分别为G,H,连接DG,DC,DH,则有DG=DH=DE,DG⊥AC,DH⊥BC.
∴
=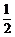 AB•DE+
AB•DE+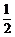 BC•DH+
BC•DH+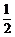 AC•DG=
AC•DG=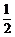 (AB+BC+AC) •DE=
(AB+BC+AC) •DE=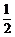 l•DE.
l•DE.
∵ =4
=4 ,∴
,∴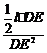 =4
=4 ,∴l=8
,∴l=8 DE.
DE.
∵CG,CH是⊙D的切线,∴∠GCD=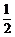 ∠ACB=30°,
∠ACB=30°,
∴在Rt△CGD中,CG= =
= =
= DE,∴CH=CG=
DE,∴CH=CG= DE.
DE.
又由切线长定理可知AG=AE,BH=BE,
∴l=AB+BC+AC=2 +2
+2 DE=8
DE=8 DE,解得DE=
DE,解得DE= ,
,
∴△ABC的周长为 .
.
[涉及知识点]垂径定理 勾股定理 内切圆 切线长定理 三角形面积
[点评]本题巧妙将垂径定理、勾股定理、内切圆、切线长定理、三角形面积等知识综合在一起,需要考生从前往后按顺序解题,前面问题为后面问题的解决提供思路,是一道难度较大的综合题
[推荐指数]★★★★★
23.(2010广东广州,23,12分)已知反比例函数y= (m为常数)的图象经过点A(-1,6).
(m为常数)的图象经过点A(-1,6).
(1)求m的值;
(2)如图9,过点A作直线AC与函数y= 的图象交于点B,与x轴交于点C,且AB=2BC,求点C的坐标.
的图象交于点B,与x轴交于点C,且AB=2BC,求点C的坐标.
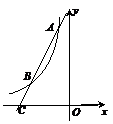

[分析](1)将A点坐标代入反比例函数解析式即可得到一个关于m的一元一次方程,求出m的值;(2)分别过点A、B作x轴的垂线,垂足分别为点D、E,则△CBE∽△CAD,运用相似三角形知识求出CE的长即可求出点C的横坐标.
[答案]解:(1)∵ 图像过点A(-1,6), . ∴
. ∴
(2)分别过点A、B作x轴的垂线,垂足分别为点D、E,


由题意得,AD=6,OD=1,易知,AD∥BE,
∴△CBE∽△CAD,∴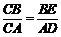 .
.
∵AB=2BC,∴
∴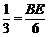 ,∴BE=2.
,∴BE=2.
即点B的纵坐标为2
当y=2时,x=-3,易知:直线AB为y=2x+8,
∴C(-4,0)
[涉及知识点]反比例函数
[点评]由于今年来各地中考题不断降低难度,中考考查知识点有向低年级平移的趋势,反比例函数出现在解答题中的频数越来约多.
[推荐指数]★★★★
22.(2010广东广州,22,12分)目前世界上最高的电视塔是广州新电视塔.如图8所示,新电视塔高AB为610米,远处有一栋大楼,某人在楼底C处测得塔顶B的仰角为45°,在楼顶D处测得塔顶B的仰角为39°.
(1)求大楼与电视塔之间的距离AC;
(2)求大楼的高度CD(精确到1米)

[分析](1)由于∠ACB=45°,∠A=90°,因此△ABC是等腰直角三角形,所以AC=AB=610;(2)根据矩形的对边相等可知:DE=AC=610米,在Rt△BDE中,运用直角三角形的边角关系即可求出BE的长,用AB的长减去BE的长度即可.
[答案](1)由题意,AC=AB=610(米);
(2)DE=AC=610(米),在Rt△BDE中,tan∠BDE=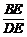 ,故BE=DEtan39°.
,故BE=DEtan39°.
因为CD=AE,所以CD=AB-DE·tan39°=610-610×tan39°≈116(米)
答:大楼的高度CD约为116米.
[涉及知识点]解直角三角形
[点评]解直角三角形是每年中考的必考知识点之一,主要考查直角三角形的边角关系及其应用,难度一般不会很大,本题是基本概念的综合题,主要考查考生应用知识解决问题的能力,很容易上手,容易出错的地方是近似值的取舍.
[推荐指数]★★★★★
21.(2010广东广州,21,12分)已知抛物线y=-x2+2x+2.
(1)该抛物线的对称轴是 ,顶点坐标 ;
(2)选取适当的数据填入下表,并在图7的直角坐标系内描点画出该抛物线的图象;
|
x |
… |
|
|
|
|
|
… |
|
y |
… |
|
|
|
|
|
… |
(3)若该抛物线上两点A(x1,y1),B(x2,y2)的横坐标满足x1>x2>1,试比较y1与y2的大小.


[分析](1)代入对称轴公式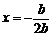 和顶点公式(-
和顶点公式(- ,
,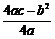 )即可;(3)结合图像可知这两点位于对称轴右边,图像随着x的增大而减少,因此y1<y2.
)即可;(3)结合图像可知这两点位于对称轴右边,图像随着x的增大而减少,因此y1<y2.
[答案]解:(1)x=1;(1,3)
(2)
|
x |
… |
-1 |
0 |
1 |
2 |
3 |
… |
|
y |
… |
-1 |
2 |
3 |
2 |
-1 |
… |
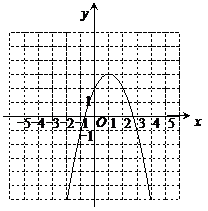

(3)因为在对称轴x=1右侧,y随x的增大而减小,又x1>x2>1,所以y1<y2.
[涉及知识点]抛物线的顶点、对称轴、描点法画图、函数增减性
[点评]二次函数是中考考查的必考内容之一,本题是综合考查二次函数的一些基础知识,需要考生熟悉二次函数的相关基本概念即可解题.
[推荐指数]★★★★★
20.(2010广东广州,20,10分)广州市某中学的一个数学兴趣小组在本校学生中开展主题为“垃圾分类知多少”的专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,划分等级后的数据整理如下表:
|
等级 |
非常了解 |
比较了解 |
基本了解 |
不太了解 |
|
频数 |
40 |
120 |
36 |
4 |
|
频率 |
0.2 |
m |
0.18 |
0.02 |
(1)本次问卷调查取样的样本容量为_______,表中的m值为_______.
(2)根据表中的数据计算等级为“非常了解”的频数在扇形统计图6所对应的扇形的圆心角的度数,并补全扇形统计图.
(3)若该校有学生1500人,请根据调查结果估计这些学生中“比较了解”垃圾分类知识的人数约为多少?
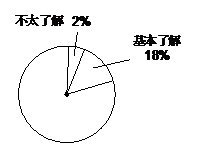
[分析](1)由于非常了解频数40,频率为0.2,因此样本容量为:40÷0.2=200,表中的m是比较了解的频率,可用频数120除以样本容量200;(2)非常了解的频率为0.2,扇形圆心角的度数为0.2×360°=72°;(3)由样本中“比较了解”的频率0.6可以估计总体中“比较了解”的频率也是0.6.
[答案](1)200;0.6;
(2)72°;补全图如下:

(3)1800×0.6=900
[涉及知识点]扇形统计图 样本估计总体
[点评]统计图表是中考的必考内容,本题渗透了统计图、样本估计总体的知识,数据的问题在中考试卷中也有越来越综合的趋势.
[推荐指数]★★★★★
19.(2010广东广州,19,10分)已知关于x的一元二次方程 有两个相等的实数根,求
有两个相等的实数根,求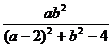 的值。
的值。
[分析]由于这个方程有两个相等的实数根,因此⊿= ,可得出a、b之间的关系,然后将
,可得出a、b之间的关系,然后将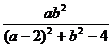 化简后,用含b的代数式表示a,即可求出这个分式的值.
化简后,用含b的代数式表示a,即可求出这个分式的值.
[答案]解:∵ 有两个相等的实数根,
有两个相等的实数根,
∴⊿= ,即
,即 .
.
∵
∵ ,∴
,∴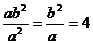
[涉及知识点]分式化简,一元二次方程根的判别式
[点评]本题需要综合运用分式和一元二次方程来解决问题,考查学生综合运用多个知识点解决问题的能力,属于中等难度的试题,具有一定的区分度.
18.(2010广东广州,18,9分)如图5,在等腰梯形ABCD中,AD∥BC.
求证:∠A+∠C=180°

[分析]由于AD∥BC,所以∠A+∠B=180°,要想说明∠A+∠C=180°,只需根据等腰梯形的两底角相等来说明∠B=∠C即可.
[答案]证明:∵梯形ABCD是等腰梯形,
∴∠B=∠C
又∵AD∥BC,
∴∠A+∠B=180°
∴∠A+∠C=180°
[涉及知识点]等腰梯形性质
[点评]本题是一个简单的考查等腰梯形性质的解答题,属于基础题.
[推荐指数]★★★
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com