
6.一元二次方程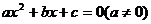 有两个不相等的实数根,则
有两个不相等的实数根,则 满足的条件是
满足的条件是
A. =0
B.
=0
B. >0
>0
C. <0 D.
<0 D. ≥0
≥0
5.如图2,火车匀速通过隧道(隧道长大于火车长)时,火车进入隧道的时间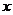 与火车在隧道内的长度
与火车在隧道内的长度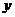 之间的关系用图象描述大致是
之间的关系用图象描述大致是

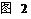



A. B. C. D.
4. 小军将一个直角三角板(如图1)绕它的一条直角边所在的直线旋转一周形成一个几何体,将这个几何体的侧面展开得到的大致图形是
小军将一个直角三角板(如图1)绕它的一条直角边所在的直线旋转一周形成一个几何体,将这个几何体的侧面展开得到的大致图形是
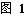




A. B. C. D.
3.下列计算正确的是
A.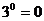 B.
B.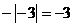 C.
C. D.
D.
2.某班体育委员记录了第一小组七位同学定点投篮(每人投10个)的情况,投进篮框的个数为6,10,5,3,4,8,4,这组数据的中位数和极差分别是
A.4,7 B.7,5 C.5,7 D.3,7
1.数轴上的点A到原点的距离是6,则点A表示的数为
A.  或
或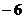 B. 6
C.
B. 6
C. 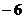 D.
D. 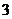 或
或
26.(本题满分10分)
如图,直线 与x轴交于点A,与y轴交于点B,以线段AB为直径作⊙C,抛物线
与x轴交于点A,与y轴交于点B,以线段AB为直径作⊙C,抛物线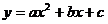 过A、C、O三点.
过A、C、O三点.
(1) 求点C的坐标和抛物线的解析式;
(2) 过点B作直线与x轴交于点D,且OB2=OA·OD,求证:DB是⊙C的切线;
(3) 抛物线上是否存在一点P, 使以P、O、C、A为顶点的四边形为直角梯形,如果存在,求出点P的坐标;如果不存在,请说明理由.
|

|
湘潭市2010年初中毕业学业考试
25.(本题满分10分)
如图,在直角梯形ABCD中,AB∥DC,∠D=90o,AC⊥BC,AB=10cm,BC=6cm,F点以2cm/秒的速度在线段AB上由A向B匀速运动,E点同时以1cm/秒的速度在线段BC上由B向C匀速运动,设运动时间为t秒(0<t<5).
(1)求证:△ACD∽△BAC;
(2)求DC的长;
(3)设四边形AFEC的面积为y,求y 关于t的函数关系式,并求出y的最小值.
|

24.(本题满分8分)
某市为了提高学生的安全防范意识和能力,每年在全市中小学学生中举行安全知识竞赛,为了了解今年全市七年级同学的竞赛成绩情况,小强随机调查了一些七年级同学的竞赛成绩,根据收集到的数据绘制了参与调查学生成绩的频数分布直方图和其中合格学生成绩的扇形统计图如下:
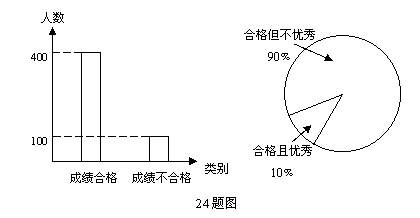

根据统计图提供的信息,解答以下问题:
(1)小强本次共调查了多少名七年级同学的成绩?被调查的学生中成绩合格的频率是多少?
(2)该市若有10000名七年级学生,请你根据小强的调查统计结果估计全市七年级学生中有多少名学生竞赛成绩合格?对此你有何看法?
(3)填写下表:
|
成绩 |
不合格 |
合格但不优秀 |
合格且优秀 |
|
频率 |
0.2 |
|
|
23.(本题满分8分)
Rt△ABC与Rt△FED是两块全等的含30o、60o角的三角板,按如图(一)所示拼在一起,CB与DE重合.
(1)求证:四边形ABFC为平行四边形;
(2)取BC中点O,将△ABC绕点O顺时钟方向旋转到如图(二)中△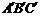 位置,直线
位置,直线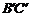 与AB、CF分别相交于P、Q两点,猜想OQ、OP长度的大小关系,并证明你的猜想.
与AB、CF分别相交于P、Q两点,猜想OQ、OP长度的大小关系,并证明你的猜想.
(3)在(2)的条件下,指出当旋转角至少为多少度时,四边形PCQB为菱形(不要求证明).
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com