
26.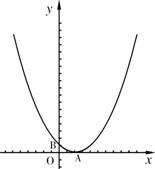 (14分)如图所示,已知抛物线
(14分)如图所示,已知抛物线 的图象与
的图象与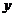 轴相交于点
轴相交于点
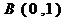 ,点
,点 在该抛物线图象上,且以
在该抛物线图象上,且以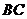 为直径的⊙
为直径的⊙ 恰
恰
好经过顶点 .
.
(1)求 的值;
的值;
(2)求点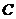 的坐标;
的坐标;
(3)若点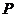 的纵坐标为
的纵坐标为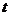 ,且点
,且点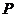 在该抛物线的对称轴
在该抛物线的对称轴 上运动,试探
上运动,试探
索:
①当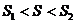 时,求
时,求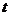 的取值范围(其中:
的取值范围(其中: 为△
为△ 的面积,
的面积, 为△
为△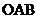 的面积,
的面积, 为四边
为四边
形OACB的面积);
②当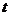 取何值时,点
取何值时,点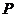 在⊙
在⊙ 上.(写出
上.(写出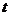 的值即可)
的值即可)
25.(12分)我们容易发现:反比例函数的图象是一个中心对称图形.你
可以利用这一结论解决问题.
如图,在同一直角坐标系中,正比例函数的图象可以看作是:将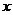 轴所在的直线绕着原点
轴所在的直线绕着原点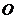 逆时针旋转α度角后的图形.若它与反比例函数
逆时针旋转α度角后的图形.若它与反比例函数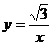 的图象分别交于第一、三象限的点
的图象分别交于第一、三象限的点 、
、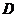 ,已知点
,已知点 、
、 .
.
(1)直接判断并填写:不论α取何值,四边形 的形状一定是
;
的形状一定是
;
(2)①当点 为
为 时,四边形
时,四边形 是矩形,试求
是矩形,试求 、α、和
、α、和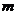 有值;
有值;
②观察猜想:对①中的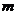 值,能使四边形
值,能使四边形 为矩形的点
为矩形的点 共有几个?(不必说理)
共有几个?(不必说理)
(3)试探究:四边形 能不能是菱形?若能, 直接写出B点的坐标, 若不能, 说明理由.
能不能是菱形?若能, 直接写出B点的坐标, 若不能, 说明理由.
24.(9分)某蔬菜公司收购到一批蔬菜,计划用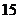 天加工后上市销售.该公司的加工能力是:每天可以精加工
天加工后上市销售.该公司的加工能力是:每天可以精加工 吨或者粗加工
吨或者粗加工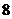 吨,且每吨蔬菜精加工后的利润为
吨,且每吨蔬菜精加工后的利润为 元,粗加工后为
元,粗加工后为 元.已知公司售完这批加工后的蔬菜,共获得利润
元.已知公司售完这批加工后的蔬菜,共获得利润 元.
元.
请你根据以上信息解答下列问题:
(1)如果精加工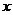 天,粗加工
天,粗加工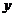 天,依题意填写下列表格:
天,依题意填写下列表格:
|
|
精加工 |
粗加工 |
|
加工的天数(天) |
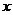 |
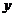 |
|
获得的利润(元) |
|
|
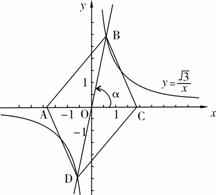 (2)求这批蔬菜共多少吨.
(2)求这批蔬菜共多少吨.
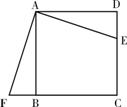
23. (9分)如图,在梯形
(9分)如图,在梯形 中,
中, ,
,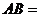
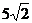 ,点
,点 在
在 上,
上,
 ,
, ,
, .
.
求: 的长及
的长及 的值.
的值.
22.(9分)在一个黑色的布口袋里装着白、红、黑三种颜色的小球,它们除了颜色之外没有其它区别,其中白球2只、红球1只、黑球1只. 袋中的球已经搅匀.
(1)随机地从袋中摸出1只球,则摸出白球的概率是多少?
(2)随机地从袋中摸出1只球,放回搅匀再摸出第二个球.请你用画树状图或列表的方法表示所有等可能的结果,并求两次都摸出白球的概率.
21.(9分)如图, 正方形 中,
中,  是
是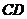 上一点,
上一点,  在
在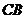 的延长线上,
的延长线上,
且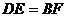 .
.
(1)求证:
 ≌
≌ ;
;
(2)问:将 顺时针旋转多少度后与
顺时针旋转多少度后与 重合,旋转中心是什么?
重合,旋转中心是什么?
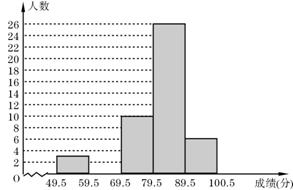
20.(9分)吴老师为了解本班学生的数学学习情况,对某次数学考试成绩(成绩取整数,满分为100分)作了统计,绘制成如下频数分布表和频数分布直方图.
请你根据图表提供的信息,解答下列问题:
(1)求频率分布表中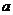 、
、 、
、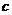 的值;并补全频数分布直方图;
的值;并补全频数分布直方图;
(2)如果用扇形统计图表示这次数学考试成绩时,那么成绩在69.5-79.5范围内的扇形圆心角的度数为多少度?
|
分组 |
49.5-59.5 |
59.5-69.5 |
69.5-79.5 |
79.5-89.5 |
89.5-100.5 |
合计 |
|
频数 |
3 |
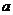 |
10 |
26 |
6 |
 |
|
频率 |
0.06 |
0.10 |
0.20 |
0.52 |
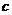 |
1.00 |
19.(9分)先化简,再求值: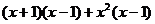 ,其中
,其中 .
.
18.(9分)计算: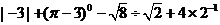 .
.
17. 如图,两同心圆的圆心为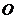 ,大圆的弦
,大圆的弦 切小圆于
切小圆于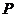 ,两圆的半径分别为
,两圆的半径分别为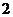
和 ,则弦长
,则弦长 = ;若用阴影部分围成一个圆锥,则该圆锥的底面半径
= ;若用阴影部分围成一个圆锥,则该圆锥的底面半径
为 .(结果保留根号)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com