
6.如图,为一个圆锥的三视图,则此圆锥的侧面积是( )

5.下列说法正确的是( )
A.有两个角为直角的四边形是矩形
B.矩形的对角线互相垂直
C.等腰梯形的对角线相等 (第4题图)
 D.对角线互相垂直的四边形是菱形
D.对角线互相垂直的四边形是菱形
4.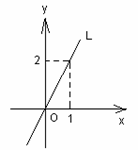 如图,把直线L沿x轴正方向向右平移2个单位得到
如图,把直线L沿x轴正方向向右平移2个单位得到
直线L′,则直线L/的解析式为( )
A.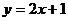 B.
B. 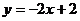
C.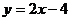 D.
D. 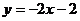
3.某鞋店试销一种新款女鞋,销售情况如下表所示:
|
型号 |
22 |
22.5 |
23 |
23.5 |
24 |
24.5 |
25 |
|
数量(双) |
3 |
5 |
10 |
15 |
8 |
3 |
2 |
鞋店经理最关心的是,哪种型号的鞋销量最大.对他来说,下列统计量中最重要的是( )
A.平均数 B.众数 C.中位数 D.方差
2.方程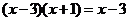 的解是( )
的解是( )
A.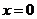 B.
B.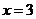 C.
C.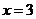 或
或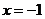 D.
D. 或
或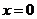
1.下列运算正确的是( )
A.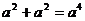 B.
B.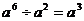 C.
C. D.
D.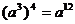
22.(满分14分)
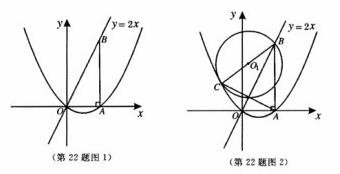
如图1,在平面直角坐标系中,点B在直线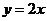 上,过点B作
上,过点B作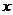 轴的垂线,垂足为A,OA=5。若抛物线
轴的垂线,垂足为A,OA=5。若抛物线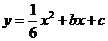 过点O、A两点。
过点O、A两点。
(1)求该抛物线的解析式;
(2)若A点关于直线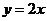 的对称点为C,判断点C是否在该抛物线上,并说明理由;
的对称点为C,判断点C是否在该抛物线上,并说明理由;
(3)如图2,在(2)的条件下,⊙O1是以BC为直径的圆。过原点O作O1的切线OP,P为切点(P与点C不重合),抛物线上是否存在点Q,使得以PQ为直径的圆与O1相切?若存在,求出点Q的横坐标;若不存在,请说明理由。




21.(满分13分)
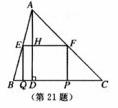
如图,在△ABC中,∠C=45°,BC=10,高AD=8,矩形EFPQ的一边QP在边上,E、F两点分别在AB、AC上,AD交EF于点H。
(1)求证: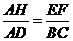 ;
;
(2)设EF=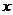 ,当
,当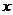 为何值时,矩形EFPQ的面积最大?并求其最大值;
为何值时,矩形EFPQ的面积最大?并求其最大值;
(3)当矩形EFPQ的面颊最大时,该矩形EFPQ以每秒1个单位的速度沿射线QC匀速运动(当点Q与点C重合时停止运动),设运动时间为t秒,矩形EFPQ与△ABC重叠部分的面积为S,求S与t的函数关系式。
20.(满分12分)
郑老师想为希望小学四年(3)班的同学购买学习用品,了解到某商店每个书包的价格比每本词典多8元,用124元恰好可以买到3个书包和2本词典。
(1)每个书包和每本词典的价格各是多少元?
(2)郑老师计划用1000元为全班40位同学没认购买一件学习用品(一个书包或一本词典)后,余下不少于100元且不超过120元的钱购买体育用品,共有哪几种购买书包和词典的方案?
19.(满分11分)
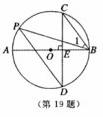 如图,AB是⊙O的直径,弦CD⊥AB与点E,点P在⊙O上,∠1=∠C,
如图,AB是⊙O的直径,弦CD⊥AB与点E,点P在⊙O上,∠1=∠C,
(1)求证:CB∥PD;
(2)若BC=3,sinP=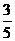 ,求⊙O的直径。
,求⊙O的直径。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com