合题意，请将正确的选项填涂到答题卡上)

1. 3的相反数是

A. 3　　　　　　　 B. -3　　　　　　　 C. 　　　　　　　 D.

25．如图，矩形ABCD (点A在第一象限)与x轴的正半轴相交于M,，与y的负半轴相交于N，

AB∥x轴，反比例函数y=的图象过A、C两点，直线AC与x轴相交于点E、与y轴相交于点F。

(1)若B(-3，3)，直线AC的解析式为y=.

①求a的值；

②连结OA、OC，若△OAC的面积记为S，△ABC的面积记为S，记S= S－S，问S是否存在最小值？若存在，求出其最小值；若不存在，请说明理由

(2)AE与CF是否相等？请证明你的结论。

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (第25题图)

24．(本小题满分12分)

某课题组在探究“泵站问题”时抽象出数学模型：

直线l同旁有两个定点A、B，在直线l上存在点P，使得PA+PB的值最小.解法：作点A关于直线l的对称点A，连接AB，则AB与直线l的交点即为P，且PA+PB的最小值为AB.

请利用上述模型解决下列问题：

(1)几何应用：如图1，等腰直角三角形ABC的直角边长为2，E是斜边AB的中点，P是AC边上的一动点，则PB+PE的最小值为　　　　　　　　　　 ；

(2)几何拓展：如图2, △ABC中，AB=2，∠BAC=30,若在AC、AB上各取一点M、N使BM+MN的值最小，求这个最小值；

(3)代数应用：求代数式(0≤x≤4)的最小值.

23．(本小题满分10分)

某水产品养殖企业为指导该企业某种水产品的养殖

和销售，对历年市场行情和水产品养殖情况进行了

调查．调查发现这种水产品的每千克售价y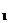(元)

与销售月份x(月)满足关系式，

而其每千克成本y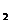(元)与销售月份x(月)满足

的函数关系，其图象如图所示．

(1)求y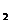的解析式；

(2)问这种水产品下半年几月份出售每千克的利润最大？最大利润是多少？

22．(本小题满分10分)

如图，以菱形ABCD的边AB为直径的⊙O交对角线

AC于点P，过P作PE⊥BC，垂足为E。

⑴求证：PE是⊙O的切线。

⑵若菱形ABCD的面积为24，tan,求PE的长.

21．(本小题满分8分)

(1)如图1，D是△ABC的边BC上的一点，且,若△ABD的面积为,△ABC的面积为S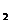，则: S =　　　　　 ；

(2)利用图1的结论在图2、3中将△ABC分别按以下两种方式分为三个面积相等的三角形，并说明分点所在的位置.

20. (本小题满分8分)

为了提高农民抵御大病风险的能力，全国农村推行了新型农村合作医疗政策，农民只需每人每年交10钱，就可以加入合作医疗，若农民患病住院治疗，出院后可到新型农村合作医疗办公室按一定比例报销医疗费.小军与同学随机调查了他们镇的一些村民，根据收集的数据制成如图所示的统计图。

根据以上信息，解答下列问题：

(1)本次共调查多少村民？有多少人参加合作医疗并的到报销款？

(2)若该镇有村民10000人，请你估计大约有多少人参加了合作医疗保险？要使两年后参加合作医疗保险的人数达到9680人，假设这两年的增长率相同，求这个年增长率.

19．(本小题满分8分)

如图，线段与相交于点，E、F分别为OB、

OC的中点，连接AB、DC、EF分别将“”

记为①，“”记为②，“”

记为③， 要求同学从这三个等式中选出两个作为条件，

一个作为结论.(在横线上填上序号)　　　　　　　　　　　　　　 (第19题图)

　(1) 写出一个真命题: 如果　　　 、　　　 　，那么　　　 　.并证明这个真命题．

(2) 写出一个假命题：如果　　　 、　　　 　，那么　　　 .　　　　　　　

18．(本小题满分8分)

解不等式，并把解集在数轴上表示出来。

17. (本小题满分8分)

已知，求的值.