
6.李大伯有一片果林,共80棵果树,某日,李大伯开始采摘今年第一批成熟的果子,他随机选取2棵果树共摘得果子,质量分别为(单位:kg):0.28,0.26,0.24,0.23,0.25,0.24,0.26,0.26,0.25,0.23,以此计算,李大伯收获的这批果子的单个质量和总质量分别约为( )
A.0.25kg,200kg B.2. 5kg,100kg C.0.25kg,100kg D.2. 5kg,200kg
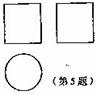
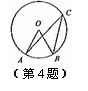
5.已知一个几何体的三视图如图所示,则该几何体是( )
A.棱柱 B.圆柱 C.圆锥 D.球
4.如图,A、B、C是⊙O上的三点,已知∠O=60º,则∠C=( )
A.20º B.25º C.30º D.45º
3.设a>0,b>0,则下列运算错误的是( )
A.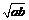 =
=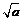 ·
·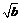 B.
B.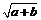 =
=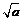 +
+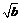 C.(
C.(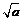 )2=a D.
)2=a D.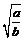 =
=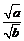
2.若分式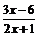 的值为0,则( )
的值为0,则( )
A.x=-2 B.x=-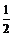 C.x=
C.x=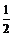 D.x=2
D.x=2
1.在直角坐标系中,点(2,1)在( )
 A.第一象限 B.第二象限 C.第三象限 D.第四象限
A.第一象限 B.第二象限 C.第三象限 D.第四象限
24. 如图,Rt△ABC中,∠C=90°,BC=6,AC=8.点P,Q都是斜边AB上的动点,点P从B 向A运动(不与点B重合),点Q从A向B运动,BP=AQ.点D,E分别是点A,B以Q,P为对称中心的对称点, HQ⊥AB于Q,交AC于点H.当点E到达顶点A时,P,Q同时停止运动.设BP的长为x,△HDE的面积为y.
如图,Rt△ABC中,∠C=90°,BC=6,AC=8.点P,Q都是斜边AB上的动点,点P从B 向A运动(不与点B重合),点Q从A向B运动,BP=AQ.点D,E分别是点A,B以Q,P为对称中心的对称点, HQ⊥AB于Q,交AC于点H.当点E到达顶点A时,P,Q同时停止运动.设BP的长为x,△HDE的面积为y.
(1)求证:△DHQ∽△ABC;
(2)求y关于x的函数解析式并求y的最大值;
(3)当x为何值时,△HDE为等腰三角形?
23.如图1,Rt△ABC≌Rt△EDF,∠ACB=∠F=90°,∠A=∠E=30°.△EDF绕着边AB的中点D旋转, DE,DF分别交线段AC于点M,K.
(1)观察: ①如图2、图3,当∠CDF=0° 或60°时,AM+CK_______MK(填“>”,“<”或“=”).
②如图4,当∠CDF=30° 时,AM+CK___MK(只填“>”或“<”).
(2)猜想:如图1,当0°<∠CDF<60°时,AM+CK_______MK,证明你所得到的结论.
 (3)如果
(3)如果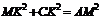 ,请直接写出∠CDF的度数和
,请直接写出∠CDF的度数和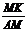 的值.
的值.
21.果农老张进行杨梅科学管理试验.把一片杨梅林分成甲、乙两部分,甲地块用新技术管理,乙地块用老方法管理,管理成本相同.在甲、乙两地块上各随机选取20棵杨梅树,根据每棵树产量把杨梅树划分成A,B,C,D,E五个等级(甲、乙的等级划分标准相同,每组数据包括左端点不包括右端点).画出统计图如下:
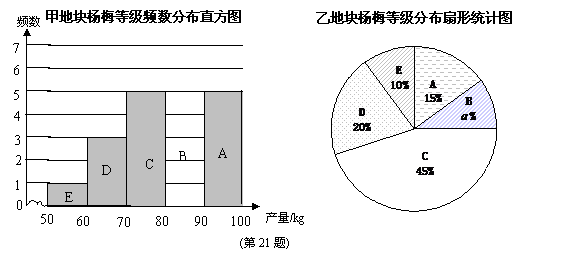
(1)补齐直方图,求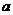 的值及相应扇形的圆心角度数;
的值及相应扇形的圆心角度数;
(2)选择合适的统计量,比较甲乙两地块的产量水平,并说明试验结果;
(3)若在甲地块随机抽查1棵杨梅树,求该杨梅树产量等级是B的概率.
22.类比学习:一动点沿着数轴向右平移3个单位,再向左平移2个单位,相当于向右平移1个单位.用实数加法表示为 3+(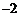 )=1.
)=1.
若坐标平面上的点作如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移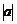 个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移
个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移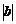 个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为
个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为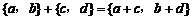 .
.
解决问题:(1)计算:{3,1}+{1,2};{1,2}+{3,1}.
(2)①动点P从坐标原点O出发,先按照“平移量”{3,1}平移到A,再按照“平移量”
{1,2}平移到B;若先把动点P按照“平移量”{1,2}平移到C,再按照“平移量”
{3,1}平移,最后的位置还是点B吗? 在图1中画出四边形OABC.
②证明四边形OABC是平行四边形.
(3)如图2,一艘船从码头O出发,先航行到湖心岛码头P(2,3),再从码头P航行到码头Q(5,5),最后回到出发点O. 请用“平移量”加法算式表示它的航行过程.

20.A,B两城相距600千米,甲、乙两车同时从A城出发驶向B城,甲车到达B城后立即返回.如图是它们离A城的距离y(千米)与行驶时间 x(小时)之间的函数图象.
(1)求甲车行驶过程中y与x之间的函数解析式,并写出自变量x的取值范围;
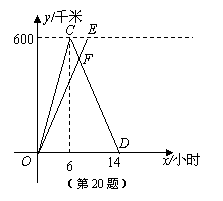 (2)当它们行驶7了小时时,两车相遇,求乙车速度.
(2)当它们行驶7了小时时,两车相遇,求乙车速度.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com