
2.集合{a,b,c }的真子集共有 个
|
运算类型 |
交 集 |
并 集 |
补 集 |
|
定 义 |
由所有属于A且属于B的元素所组成的集合,叫做A,B的交集.记作A B(读作‘A交B’),即A B(读作‘A交B’),即A B={x|x B={x|x A,且x A,且x B}. B}. |
由所有属于集合A或属于集合B的元素所组成的集合,叫做A,B的并集.记作:A B(读作‘A并B’),即A B(读作‘A并B’),即A B ={x|x B ={x|x A,或x A,或x B}). B}). |
设S是一个集合,A是S的一个子集,由S中所有不属于A的元素组成的集合,叫做S中子集A的补集(或余集) 记作 记作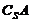 ,即 ,即CSA=  |
|
韦 恩 图 示 |
 |
 |
  |
|
性 质 |
A A=A A=A A  Φ=Φ Φ=ΦA  B=B B=B A AA  B B A AA  B B B B |
A A=A A=AA  Φ=A Φ=AA  B=B B=B A AA  B B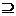 A AA  B B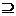 B B |
(CuA)  (CuB) (CuB)= Cu (A  B) B)(CuA)  (CuB) (CuB)= Cu(A  B) B)A  (CuA)=U (CuA)=UA  (CuA)=
Φ. (CuA)=
Φ. |
例题:
1.下列四组对象,能构成集合的是 ( )
A某班所有高个子的学生 B著名的艺术家 C一切很大的书 D 倒数等于它自身的实数
3. 不含任何元素的集合叫做空集,记为Φ
规定: 空集是任何集合的子集, 空集是任何非空集合的真子集。
u 有n个元素的集合,含有2n个子集,2n-1个真子集
2.“相等”关系:A=B (5≥5,且5≤5,则5=5)
实例:设 A={x|x2-1=0} B={-1,1} “元素相同则两集合相等”
即:① 任何一个集合是它本身的子集。AÍA
②真子集:如果AÍB,且A¹ B那就说集合A是集合B的真子集,记作A B(或B
B(或B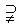 A)
A)
③如果 AÍB, BÍC ,那么 AÍC
④ 如果AÍB 同时 BÍA 那么A=B
1.“包含”关系-子集
注意: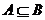 有两种可能(1)A是B的一部分,;(2)A与B是同一集合。
有两种可能(1)A是B的一部分,;(2)A与B是同一集合。
反之: 集合A不包含于集合B,或集合B不包含集合A,记作A B或B
B或B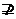 A
A
4、集合的分类:
(1) 有限集 含有有限个元素的集合
(2) 无限集 含有无限个元素的集合
(3) 空集 不含任何元素的集合 例:{x|x2=-5}
3.集合的表示:{ … } 如:{我校的篮球队员},{太平洋,大西洋,印度洋,北冰洋}
(1) 用拉丁字母表示集合:A={我校的篮球队员},B={1,2,3,4,5}
(2) 集合的表示方法:列举法与描述法。
u 注意:常用数集及其记法:
非负整数集(即自然数集) 记作:N
正整数集 N*或 N+ 整数集Z 有理数集Q 实数集R
1) 列举法:{a,b,c……}
2) 描述法:将集合中的元素的公共属性描述出来,写在大括号内表示集合的方法。{xÎR| x-3>2} ,{x| x-3>2}
3) 语言描述法:例:{不是直角三角形的三角形}
4) Venn图:
2. 集合的中元素的三个特性:
(1) 元素的确定性如:世界上最高的山
(2) 元素的互异性如:由HAPPY的字母组成的集合{H,A,P,Y}
(3) 元素的无序性: 如:{a,b,c}和{a,c,b}是表示同一个集合
1. 集合的含义
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com