
2.下列各组词语中没有错别字的一组是 ( )
A.磋商 举步为艰 仗势欺人 自鸣不凡
B.誊写 却之不恭 断章取意 博闻强识
C.肄业 唾手可得 应接不暇 恣意妄为
D.推诿 亦步亦趋 层峦叠嶂 头晕目炫
1.下列词语中加点的字,每对的读音都不相同的一项是 ( )
A.摒弃/摈弃 香茗/铭记 埋怨/阴霾 累赘/伤痕累累
B.舍利/舍弃 逐渐/渐染 昏厥/倔强 朔风/探本溯源
C.纰漏/倾圯 瘦削/削减 供应/供品 蜿蜒/剜肉补疮
D.曲线/龋齿 惺松/芯片 行头/行家 箴言/三缄其口
5.函数的模型

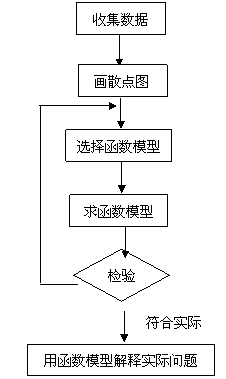
4、二次函数的零点:
二次函数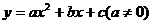 .
.
(1)△>0,方程 有两不等实根,二次函数的图象与
有两不等实根,二次函数的图象与 轴有两个交点,二次函数有两个零点.
轴有两个交点,二次函数有两个零点.
(2)△=0,方程 有两相等实根,二次函数的图象与
有两相等实根,二次函数的图象与 轴有一个交点,二次函数有一个二重零点或二阶零点.
轴有一个交点,二次函数有一个二重零点或二阶零点.
(3)△<0,方程 无实根,二次函数的图象与
无实根,二次函数的图象与 轴无交点,二次函数无零点.
轴无交点,二次函数无零点.
3、函数零点的求法:
1 (代数法)求方程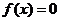 的实数根;
的实数根;
2 (几何法)对于不能用求根公式的方程,可以将它与函数 的图象联系起来,并利用函数的性质找出零点.
的图象联系起来,并利用函数的性质找出零点.
2、函数零点的意义:函数 的零点就是方程
的零点就是方程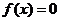 实数根,亦即函数
实数根,亦即函数 的图象与
的图象与 轴交点的横坐标。
轴交点的横坐标。
即:方程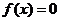 有实数根
有实数根 函数
函数 的图象与
的图象与 轴有交点
轴有交点 函数
函数 有零点.
有零点.
1、函数零点的概念:对于函数 ,把使
,把使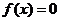 成立的实数
成立的实数 叫做函数
叫做函数 的零点。
的零点。
(三)幂函数
1、幂函数定义:一般地,形如
 的函数称为幂函数,其中
的函数称为幂函数,其中 为常数.
为常数.
2、幂函数性质归纳.
(1)所有的幂函数在(0,+∞)都有定义并且图象都过点(1,1);
(2)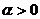 时,幂函数的图象通过原点,并且在区间
时,幂函数的图象通过原点,并且在区间 上是增函数.特别地,当
上是增函数.特别地,当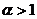 时,幂函数的图象下凸;当
时,幂函数的图象下凸;当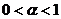 时,幂函数的图象上凸;
时,幂函数的图象上凸;
(3) 时,幂函数的图象在区间
时,幂函数的图象在区间 上是减函数.在第一象限内,当
上是减函数.在第一象限内,当 从右边趋向原点时,图象在
从右边趋向原点时,图象在 轴右方无限地逼近
轴右方无限地逼近 轴正半轴,当
轴正半轴,当 趋于
趋于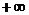 时,图象在
时,图象在 轴上方无限地逼近
轴上方无限地逼近 轴正半轴.
轴正半轴.
例题:
1. 已知a>0,a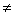 0,函数y=ax与y=loga(-x)的图象只能是 ( )
0,函数y=ax与y=loga(-x)的图象只能是 ( )

2.计算: ① ;②
;②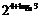 = ;
= ; =
;
=
;
③ =
=
3.函数y=log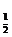 (2x2-3x+1)的递减区间为
(2x2-3x+1)的递减区间为
4.若函数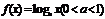 在区间
在区间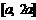 上的最大值是最小值的3倍,则a=
上的最大值是最小值的3倍,则a=
5.已知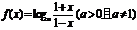 ,(1)求
,(1)求 的定义域(2)求使
的定义域(2)求使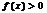 的
的 的取值范围
的取值范围
第三章 函数的应用
(二)对数函数
1、对数函数的概念:函数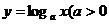 ,且
,且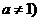 叫做对数函数,其中
叫做对数函数,其中 是自变量,函数的定义域是(0,+∞).
是自变量,函数的定义域是(0,+∞).
注意:1 对数函数的定义与指数函数类似,都是形式定义,注意辨别。如: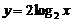 ,
,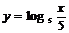 都不是对数函数,而只能称其为对数型函数.
都不是对数函数,而只能称其为对数型函数.
2 对数函数对底数的限制: ,且
,且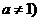 .
.
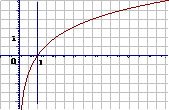
2、对数函数的性质:
|
a>1 |
0<a<1 |
|
 |
 |
|
|
定义域x>0 |
定义域x>0 |
|
|
值域为R |
值域为R |
|
|
在R上递增 |
在R上递减 |
|
|
函数图象都过定点(1,0) |
函数图象都过定点(1,0) |
(二)对数的运算性质
如果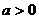 ,且
,且 ,
,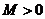 ,
, ,那么:
,那么:
1 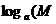 ·
·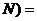
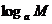 +
+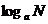 ;
;
2 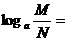
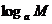 -
-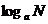 ;
;
3 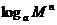

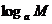
 .
.
注意:换底公式
 (
(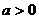 ,且
,且 ;
; ,且
,且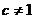 ;
; ).
).
利用换底公式推导下面的结论
(1) ;(2)
;(2)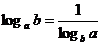 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com