
4、平面向量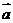 ,
, 共线的充要条件是---------------------------------------------------------------( )
共线的充要条件是---------------------------------------------------------------( )
A、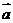 ,
, 方向相同
B、
方向相同
B、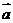 ,
, 两向量中至少有一个为零向量
两向量中至少有一个为零向量
C、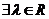 ,
,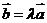 D、存在不全为零的实数
D、存在不全为零的实数 、
、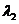 ,
,
3、命题“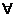
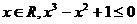 ”的否定是 --------------------------------------------------- ( )
”的否定是 --------------------------------------------------- ( )
A、存在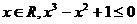 B、
B、

C、
 D、
D、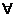

2、已知集合 -------------- ( )
-------------- ( )
A、 B、
B、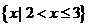 C、
C、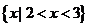 D、
D、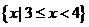
1、已知集合A={1,2,3,4},那么A的真子集的个数是-------------------------------------( )
A、15 B、16 C、7 D、8
21. (本题满分13分)设函数 是
是 上的单调递增函数,当
上的单调递增函数,当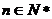 时,
时, 
 ,
,
且对于任意的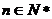 ,都有
,都有 .
.
(1)求证: (
(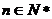 );21世纪教育网
);21世纪教育网
(2)设 (
(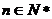 ),试证明:
),试证明: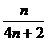 ≤
≤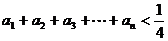 .
.
解:(1)①当 时,
时, 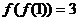 ,若
,若  ,则
,则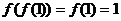 ,此与
,此与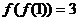 矛盾,
矛盾,
因此,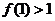 ,即
,即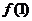 ≥2,由函数
≥2,由函数 是
是 上的单调递增函数,得
上的单调递增函数,得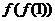 ≥
≥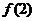
即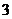 ≥
≥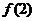 ,所以,
,所以,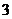 ≥
≥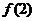
 ≥2,又当
≥2,又当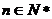 时,
时, 
 ,因此有
,因此有
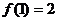 ,
,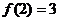 ,故当
,故当 时,等式成立;
时,等式成立;
② 假设当 时,等式成立,即
时,等式成立,即 ,亦即
,亦即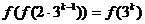 ,
,
那么当 时,由已知对于任意的
时,由已知对于任意的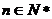 ,都有
,都有 ,
,
得 ,即
,即 ,
,
因而有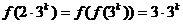
 ,所以,
,所以, 时,等式也成立.
时,等式也成立.
综合①②得 等式 对任意的
对任意的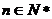 都成立.
(6分)
都成立.
(6分)
(2)由(1)得 ,所以
,所以 ,
,
而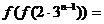
 ,因此,
,因此,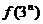
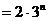 ,
,
所以,
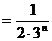 ,应用等比数列求和公式
,应用等比数列求和公式
得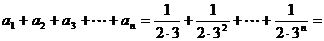
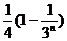
由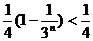 ,得
,得 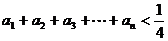 ①
①
由 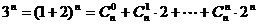 ≥
≥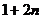 ,
,
得 ,21世纪教育网
,21世纪教育网
即 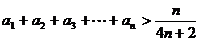 ②
②
综合①②,即有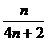 ≤
≤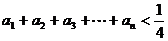 成立。 (7分)
成立。 (7分)
20. (本题满分13分)今有5封不同的信,投入三个不同的信箱,且每封信投入每个信箱的机会均等,设 是这三个信箱中某个箱子里放入最多的信件数.求
是这三个信箱中某个箱子里放入最多的信件数.求 的分布列和均值
的分布列和均值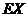 .
.
解: 的分布列为:
的分布列为:
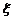 |
2 |
3 |
4 |
5 |
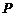 |
 |
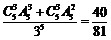 |
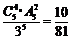 |
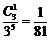 |
(10分)
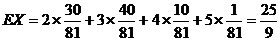 .
(3分)
.
(3分)
19.(本题满分13分)设直线 的参数方程为
的参数方程为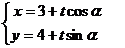
 为参数,
为参数, 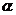 为倾斜角),
为倾斜角),
圆 的参数方程为
的参数方程为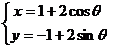 (
( 为参数)
为参数)
(1)
若直线 经过圆
经过圆 的圆心,求直线
的圆心,求直线 的斜率.
的斜率.
(2)
若直线 与圆
与圆 交于两个不同的点,求直线
交于两个不同的点,求直线 的斜率的取值范围.
的斜率的取值范围.
解:(1)由已知得
直线 经过的定点是
经过的定点是 ,而圆
,而圆 的圆心是
的圆心是
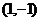 ,
,
所以,当直线 经过圆
经过圆 的圆心时,直线
的圆心时,直线 的斜率为
的斜率为 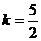 ; (5分)
; (5分)
(2)方法1. 由圆 的参数方程
的参数方程 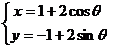 得圆
得圆 的圆心是
的圆心是
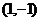 ,半径为2,
,半径为2,
由直线 的参数方程为
的参数方程为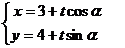
 为参数,
为参数, 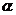 为倾斜角),
为倾斜角),
得直线 的普通方程为
的普通方程为  ,即
,即 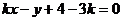 ,
,
当直线 与圆
与圆 交于两个不同的点时,圆心到直线的距离小于圆的半径,
交于两个不同的点时,圆心到直线的距离小于圆的半径,
即 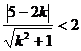 ,由此解得
,由此解得 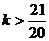 .直线
.直线 的斜率的取值范围为
的斜率的取值范围为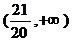 .
.
(8分) 21世纪教育网
方法2.将圆 的参数方程为
的参数方程为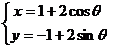
化成普通方程是  , ①
, ①
将直线 的参数方程代入①式,得
的参数方程代入①式,得 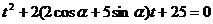 ②
②
当直线 与圆
与圆 交于两个不同的点时,方程②有两个不相等的实根,
交于两个不同的点时,方程②有两个不相等的实根,
即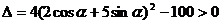 , 即
, 即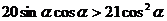 ,两边同除以
,两边同除以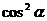 ,
,
由此解得 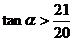 ,即直线
,即直线 的斜率的取值范围为
的斜率的取值范围为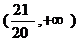 .
(8分)
.
(8分)
18. (本题满分12分)
已知对于任意实数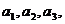 有下列不等式:
有下列不等式:
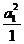 ≥
≥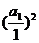 ;
;
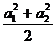 ≥
≥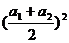 ; 21世纪教育网
; 21世纪教育网
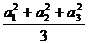 ≥
≥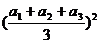 .
.
(1) 请从上述不等式中,归纳出一个对任意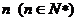 个实数
个实数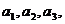
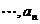 都成立的不等式:
都成立的不等式:
(2) 请证明你归纳的不等式是恒成立的。
解:(1)对任意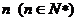 个实数
个实数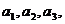
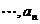 都成立的不等式是:
都成立的不等式是:
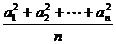 ≥
≥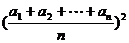 .
(3分)
.
(3分)
(2)证法1: (应用柯西不等式) 由柯西不等式 得
 ≥
≥ ,
,
两边同除以 ,即得
,即得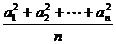 ≥
≥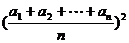 .
(9分)
.
(9分)
证法2: (应用数学归纳法)
(1) 当 时,
时, 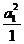 ≥
≥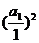 成立;
成立;
(2) 假设当 时不等式成立,即有
时不等式成立,即有 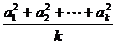 ≥
≥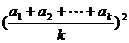 ,
,
那么, 当 时,
时, 
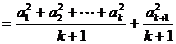
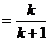
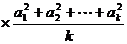
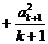 ≥
≥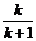
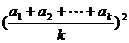
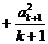

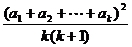
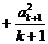 。
。
而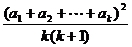
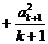


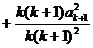
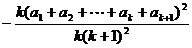
 ≥
≥ .
.
故当 时,不等式成立.
时,不等式成立.
综合(1)(2)得不等式 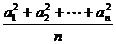 ≥
≥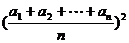 对任意
对任意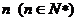 个
个
实数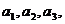
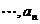 都成立.
(9分)
都成立.
(9分)
17. (本题满分12分) 设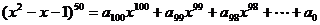 .
.
(1)求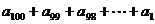 的值; (2)求
的值; (2)求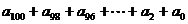 的值.
的值.
解:(1)令 ,得
,得  ;
(2分)
;
(2分)
令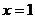 ,得
,得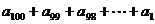
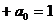 ,所以
,所以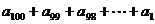
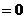 ; (4分)
; (4分)
(2)令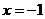 ,得
,得 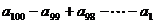
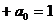 , ①
, ①
而 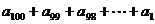
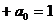 , ②
, ②
① + ② 得 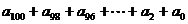
 。
( 6分)
。
( 6分)
16.(本题满分12分)
已知命题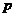 :
:  . 命题
. 命题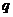 :
: ,使得
,使得 .
.
若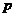 或
或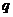 为真,
为真,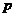 且
且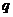 为假,求实数
为假,求实数 的取值范围.
的取值范围.
解:若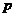 真,则
真,则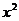 的最小值≥
的最小值≥ ,即1≥
,即1≥ ;
(2分)
;
(2分)
若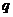 真,则
真,则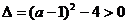 ,即
,即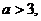 或
或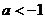 ;
(2分)
;
(2分)
若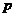 或
或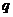 为真,
为真,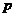 且
且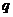 为假,则
为假,则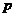 与
与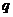 为一真一假。
(2分)
为一真一假。
(2分)
当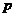 真
真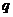 假时,有 -1≤
假时,有 -1≤ ≤1; (2分)
≤1; (2分)
当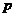 假
假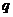 真时,有
真时,有
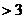 .
(2分)
.
(2分)
故当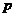 或
或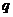 为真,
为真,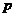 且
且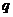 为假时, -1≤
为假时, -1≤ ≤1 或
≤1 或
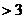 .
(2分)
.
(2分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com