
5.参数方程为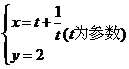 表示的曲线是( )21世纪教育网
表示的曲线是( )21世纪教育网
A.一条直线 B.两条直线 C.一条射线 D.两条射线
4、已知点M的极坐标为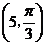 ,下列所给出的四个坐标中能表示点M的坐标是( )。
,下列所给出的四个坐标中能表示点M的坐标是( )。
A.  B.
B.
 C.
C.
 D.
D.

2、下列各式中,最小值等于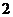 的是( )
的是( )
A  B
B  C
C  D
D 
3、函数 的最小值为( )
的最小值为( )
A 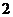 B
B 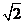 C
C 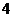 D
D 
1.在极坐标系中与圆 相切的一条直线的方程为( )
相切的一条直线的方程为( )
A.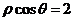 B.
B.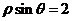 C.
C. D.
D.
21.解(I)由 ,得
,得
由 ,得
,得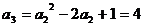
由 ,得
,得
由此猜想 的一个通项公式:
的一个通项公式: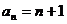 (
(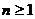 )
)
(II)(i)用数学归纳法证明:
①当 时,
时,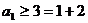 ,不等式成立.
,不等式成立.
②假设当 时不等式成立,即
时不等式成立,即 ,那么
,那么
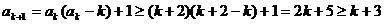 .
.
也就是说,当 时,
时,
据①和②,对于所有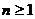 ,有
,有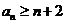 .
.
(ii)由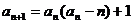 及(i),对
及(i),对 ,有
,有
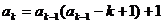

……
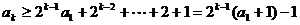
于是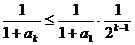 ,
,
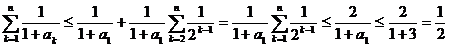
20.
解:(Ⅰ)因为对任意xεR,有f(f(x)- x2 + x)=f(x)- x2 +x,所以
f(f(2)- 22+2)=f(2)- 22+2.
又由f(2)=3,得f(3-22+2)-3-22+2,即f(1)=1.
若f(0)=a,则f(a-02+0)=a-02+0,即f(a)=a.
(Ⅱ)因为对任意xεR,有f(f(x))- x2 +x)=f(x)- x2 +x.
又因为有且只有一个实数x0,使得f(x0)- x0.
所以对任意xεR,有f(x)- x2 +x= x0.
在上式中令x= x0,有f(x0)-x + x0= x0,
+ x0= x0,
又因为f(x0)-
x0,所以x0- x =0,故x0=0或x0=1.
=0,故x0=0或x0=1.
若x0=0,则f(x)- x2 +x=0,即
f(x)= x2 –x.
但方程x2 –x=x有两上不同实根,与题设条件矛质,故x2≠0.
若x2=1,则有f(x)- x2 +x=1,即f(x)= x2 –x+1.易验证该函数满足题设条件.
综上,所求函数为
f(x)= x2 –x+1(x R).
R).
19.解:
(Ⅰ)由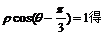

从而C的直角坐标方程为

(Ⅱ)M点的直角坐标为(2,0)N点的直角坐标为
所以P点的直角坐标为
所以直线OP的极坐标方程为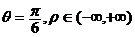
18. (Ⅰ)如图,设F为AD延长线上一点
∵A,B,C,D四点共圆,∴∠CDF=∠ABC
又AB=AC ∴∠ABC=∠ACB,且∠ADB=∠ACB, ∴∠ADB=∠CDF,
对顶角∠EDF=∠ADB, 故∠EDF=∠CDF,即AD的延长线平分∠CDE.
(Ⅱ)设O为外接圆圆心,连接AO交BC于H,则AH⊥BC.
连接OC,A由题意∠OAC=∠OCA=150, ∠ACB=750,∴∠OCH=600.
设圆半径为r,则r+ r=2+
r=2+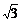 ,a得r=2,外接圆的面积为4
,a得r=2,外接圆的面积为4 。
。
17.解:
(Ⅰ)当a=-1时,f(x)=︱x-1︳+︱x+1︳.由f(x)≥3得
︱x-1︳+︱x+1|≥3x≤-1时,不等式化为1-x-1-x≥3 即-2x≥3
不等式组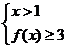 的解集为[
的解集为[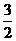 ,+∞),综上得,
,+∞),综上得,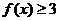 的解集为
的解集为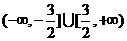
(Ⅱ)若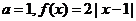 ,不满足题设条件
,不满足题设条件
若
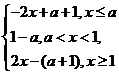 ,
, 的最小值为
的最小值为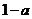
若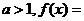
 ,
, 的最小值为
的最小值为
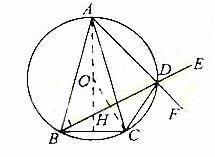 所以
所以 的充要条件是|
的充要条件是|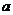 -1|≥2,从而
-1|≥2,从而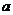 的取值范围为
的取值范围为
16. 解:(1)直线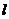 的方程为
的方程为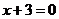 或
或 .
.
(2)若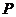 为
为 的中点,所以
的中点,所以 ,
,
由(1)知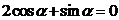 ,得
,得 ,
,
故所求弦 的方程为
的方程为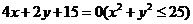 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com