
小故事:
三个古希腊哲学家,由于争论和天气炎热感到疲倦了,于是在花园里的一棵大树下躺下来休息一会,结果都睡着了.这时一个爱开玩笑的人用炭涂黑了他们的前额.三个人醒来以后,彼此看了看,都笑了起来.但这并没引起他们之中任何一个人的担心,因为每个人都以为是其他两人在互相取笑.这时其中有一个突然不笑了,因为他发觉自己的前额也给涂黑了.那么他是怎样觉察到的呢?你能想出来吗?
答案:为了方便,用甲、乙、丙分别代表三个科学家,并不妨设甲已发觉自己的脸给涂黑了.那么甲这样想:“我们三个人都可以认为自己的脸没被涂黑,如果我的脸没被涂黑,那么乙能看到(当然对于丙也是一样),乙既然看到了我的脸没给涂黑,同时他又认为他的脸也没给涂黑,那么乙就应该对丙的发笑而感到奇怪.因为在这种情况下(甲、乙的脸都是干净的),丙是没有可笑的理由了.然而现在的事实是乙对丙的发笑并不感到奇怪,可见乙是在认为丙在笑我.由此可知,我的脸也给涂黑了.
这里应着重指出的是,甲并没有直接看到自己的脸是否给涂黑了,他是根据乙、丙两人的表情进行分析、思考,而说明了自己的脸给涂黑了.简单地说,甲是通过说明脸被涂黑了的反面-没被涂黑是错误的,从而觉察了自己的脸被涂黑了.因此这是一种间接的证明方法.显然这种证明方法也是不可缺少的.
像这样,为了说明某一个结论是正确的,但不从正面直接说明,而是通过说明它的反面是错误的,从而断定它本身是正确的方法,就叫做“反证法“.
补充题:
1.若a2能被2整除,a是整数,求证:a也能被2整除.
证:假设a不能被2整除,则a必为奇数,
故可令a=2m+1(m为整数),
由此得a2=(2m+1)2=4m2+4m+1=4m(m+1)+1,
此结果表明a2是奇数,
这与题中的已知条件(a2能被2整除)相矛盾,
∴a能被2整除.
2.写出命题:“若 xy = 6则 x = 3且 y = 2”的逆命题否命题逆否命题,并判断它们的真假
解:逆命题:若 x = 3 且 y = 2 则 x + y = 5 (真)
否命题:若 x + y ¹ 5 则 x ¹ 3且y¹2 (真)
逆否命题:若 x ¹ 3 或y¹2 则 x + y ¹5 (假)
1.命题“若 x = y 则 |x| = |y|”写出它的逆命题、否命题、逆否命题,并判断它的真假
解:逆命题:若 |x| = |y| 则 x = y (假,如 x = 1, y = -1)
否命题:若 x ¹ y 则 |x| ¹|y| (假,如 x = 1, y = -1)
逆否命题:若 |x| ¹|y| 则 x ¹ y (真)
提示:1.设b2-4ac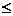 0,则方程没有实数根,或方程有两个相等的实数根,得出矛盾.
0,则方程没有实数根,或方程有两个相等的实数根,得出矛盾.
2.设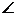 B
B 900,则
900,则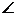 C+
C+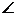 B
B 1800,得出矛盾.
1800,得出矛盾.
补充题:
反证法的基本原理及其四个步骤
例1.判断以下四种命题的真假
原命题:若四边形ABCD为平行四边形,则对角线互相平分 真
逆命题:若四边形ABCD对角线互相平分,则它为平行四边形; 真
否命题:若四边形ABCD不是为平行四边形,则对角线不平分; 真
逆否命题:若四边形ABCD对角线不平分,则它不是平行四边形; 真
归纳小结:(学生回答,教师整理补充)
(1)原命题为真,它的逆命题不一定为真;
(2)原命题为真,它的否命题不一定为真;
(3)原命题为真,它的逆否命题一定为真
结论:两个互为逆否的命题同真或同假(如原命题和它的逆否命题,逆命题和否命题),其余情况则不一定同真或同假(如原命题和逆命题,否命题和逆否命题等),这时称互为逆否的两个命题等价,即原命题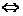 逆否命题
逆否命题
例2.(课本第32页例2)设原命题是“当c>0时,若a>b,则ac>bc”,写出它的逆命题、否命题与逆否命题,并分别判断它们的真假.
分析:“当c>0时”是大前提,写其他命题时应该保留,原命题的条件是a>b,结论是ac>bc.
解:逆命题:当c>0时,若ac>bc,则a>b.它是真命题;
否命题:当c>0时,若a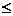 b,则ac
b,则ac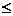 bc.它是真命题;
bc.它是真命题;
逆否命题:当c>0时,若ac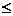 bc,则a
bc,则a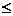 b.它是真命题.
b.它是真命题.
练习:课本第32页 练习:1,2.
答案:1.(1)正确;(2)正确.
2.(1)逆命题:两个全等三角形的三边对应相等.逆命题为真;
否命题:三边不对应相等的两个三角形不全等.否命题为真;
逆否命题:两个不全等的三角形的三边不对应相等.逆否命题为真.
(2) 逆命题:若a+c>b+c,则a>b.逆命题为真.
否命题:若a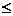 b,则a+c
b,则a+c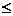 b+c.否命题为真.
b+c.否命题为真.
逆否命题:若a+c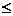 b+c,则a
b+c,则a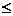 b.逆否命题为真.
b.逆否命题为真.
例3.(课本第32页例3)用反证法证明:如果a>b>0,那么 .
.
证明:假设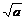 不大于
不大于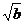 ,则或者
,则或者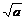 <
<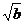 ,或者
,或者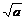 =
=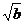 .
.
∵a>0,b>0,
∴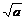 <
<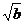

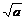
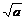 <
<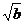
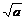 ,
,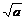
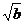 <
<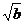
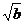

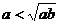 ,
,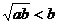
 a<b;
a<b;
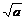 =
=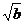
 a=b.这些都同已知条件a>b>0矛盾,∴
a=b.这些都同已知条件a>b>0矛盾,∴ .
.
证法二(直接证法)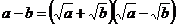 ,
,
∵a>b>0,∴a - b>0即
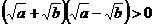 ,∴
,∴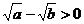
∴
例4(课本第33页例4)用反证法证明:圆的两条不是直径的相交弦不能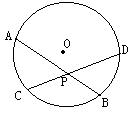 互相平分.
互相平分.
已知:如图,在⊙O中,弦AB、CD交于P,且AB、CD不是直径.
求证:弦AB、CD不被P平分.
分析:假设弦AB、CD被P平分,连结OP后,可推出AB、CD都与OP垂直,则出现矛盾.
证明:假设弦AB、CD被P平分,由于P点一定不是圆心O,连结OP,根据垂径定理的推论,
有OP⊥AB,OP⊥CD,即过点P有两条直线与OP都垂直,
这与垂线性质矛盾.
∴弦AB、CD不被P平分.
4.反证法的步骤:
(1)假设命题的结论不成立,即假设结论的反面成立
(2)从这个假设出发,通过推理论证,得出矛盾
(3)由矛盾判定假设不正确,从而肯定命题的结论正确
注意:可能出现矛盾四种情况:
①与题设矛盾;②与反设矛盾;③与公理、定理矛盾④在证明过程中,推出自相矛盾的结论
3.反证法:
要证明某一结论A是正确的,但不直接证明,而是先去证明A的反面(非A)是错误的,从而断定A是正确的即反证法就是通过否定命题的结论而导出矛盾来达到肯定命题的结论,完成命题的论证的一种数学证明方法
2.四种命题的真假关系
一个命题的真假与其他三个命题的真假有如下三条关系:
①、原命题为真,它的逆命题不一定为真
②、原命题为真,它的否命题不一定为真
③、原命题为真,它的逆否命题一定为真
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com