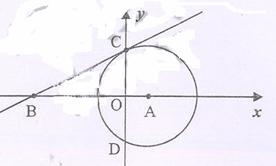
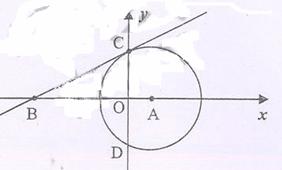
24、(本小题13分)已知：如图，⊙A与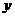轴交于C、D两点，圆心A的坐标为(1，0)，

⊙A的半径为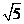，过点C作⊙A的切线交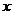于点B(－4，0)。

(1)求切线BC的解析式；

(2)若点P是第一象限内⊙A上一点，过点P作⊙A的切线与直线BC相交于点G，且∠CGP=120°，求点G的坐标；

(3)向左移动⊙A(圆心A始终保持在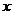上)，与直线BC交于E、F，在移动过程中是否存在点A，使得△AEF是直角三角形？若存在，求出点A 的坐标，若不存在，请说明理由。

23、(本小题9分)今年四月份，李大叔收获洋葱30吨，黄瓜13吨。现计划租用甲、乙两种货车共10辆将这两种蔬菜全部运往外地销售，已知一辆甲种货车可装洋葱4吨和黄瓜1吨，一辆乙种货车可装洋葱和黄瓜各2吨。

(1)李大叔安排甲、乙两种货车时有几种方案.请你帮助设计出来；

(2)若甲种货车每辆要付运费2000元，乙种货车每辆付运费1300元，请你帮助李大叔算一算应选哪种方案，才能使运费最少？最少运费是多少？

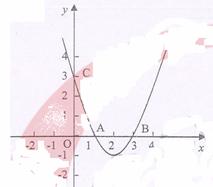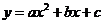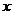22、(本小题8分)已知：如图，抛物线与轴相交于两点A(1,0),B(3,0).与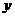轴相较于点C(0，3).

(1)求抛物线的函数关系式；

(2)若点D(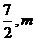)是抛物线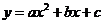上一点，请求出的值，并求处此时△ABD 的面积。

21、(本小题9分)在2009年楚雄州“火把节”房交会期间，某房地产公司对参加本次房交会的消费者进行了随机的问卷调查，共发放1000份调查问卷，并全部收回。

根据问卷调查，将消费者年收入的情况整理后，制成表格如下：

根据调查问卷，将消费者打算购买住房面积的情况整理后，作出部分频数分布直方图和扇形统计图。

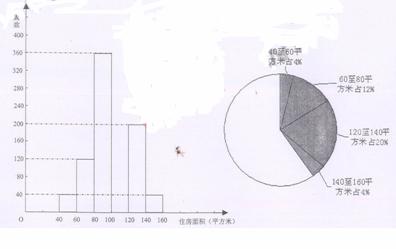
注：每组包含最小值不包含最大值，且住房面积取整数

根据以上信息回答下列问题：

(1)根据表格可得a=　　 ，被调查的1000名消费者的平均年收入为　　　 万元，

(2)补全频数分布直方图和扇形统计图。

(3)若楚雄州现有购房打算的约有40000人，请估计购房面积在80至120平方米的大约有多少人？

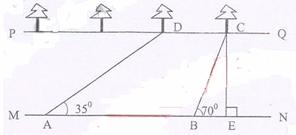
20、(本小题8分)如图，河流的两岸PQ，MN互相平行，河岸PQ上有一排小树，已知相邻两树之间的距离CD=50米，某人在河岸MN的A处测的∠DAN=35°，然后沿河岸走了120米到达B处，测的∠CBN=70°，求河流的宽度CE(结果保留两个有效数字)。

(参考数据：sin35°≈0.57，cos35°≈0.82，tan35°≈0.70

Sin70°≈0.94，cos70°≈0.34，tan70°≈2.75)

19、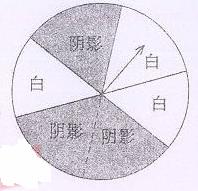(本小题8分)小明和小华为了获得一张2010年上海世博园门票，他们各自设计了一个方案：

　小明的方案是：转动如图所示的转盘，当转盘停止转动后，如果指针停在阴影区域，则小明获得门票；如果指针停在白色区域，则小华获得门票(转盘被等分成6个扇区，若指针停在边界处，则重新转动转盘)。

小华的方案是：有三张卡片，上面分别标有数字1，2，3，将它门背面朝上洗匀后，从中摸出一张，记录下卡片上的数字后放回，重新洗匀后再摸出一张，若摸出两张卡片上的数字之和为偶数，则小华获得门票。

(1)在小明的方案中，计算小明获得门票的概率，并说明小明的方案是否公平？

(2)用树状图或列表法例举小华设计方案中可能出现的所有结果，计算小华获得门票的概率，并说明小华的方案是否公平？

18、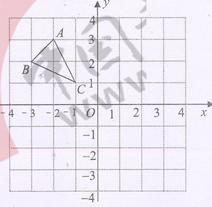(本小题7分)△ABC在平面直角坐标系中的位置如图所示

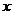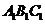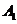(1)作出△ABC关于轴对称的△,并写出点的坐标；

(2)作出将△ABC 绕点O顺时针旋转180°后的△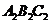

17、(本小题7分)如图，点A、E、B、D在同一条直线上，AE=DB，AC=DF，AC∥DF.

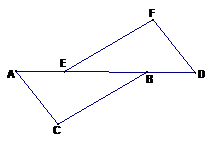请探索BC与EF有怎样的位置关系？并说明理由。

16、(本小题6分)先化简，再求值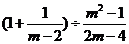：，其中。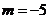

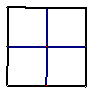
15、如图，用火柴摆出一列正方形图案，若按这种方式摆下去，摆出第n个图案用　　 根火柴棍(用含n的代数式表示)