
2.把不等式x+2>4的解表示在数轴上,正确的是()


1.给出四个数0,,-,0.3,其中最小的是()
A.0 B. C.- D.0.3
24. (本小题满分12分)
 (第24题) |
(1) ∵OABC是平行四边形,∴AB∥OC,且AB = OC = 4,
∵A,B在抛物线上,y轴是抛物线的对称轴,
∴ A,B的横坐标分别是2和– 2,
代入y =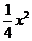 +1得, A(2, 2 ),B(–
2,2),
+1得, A(2, 2 ),B(–
2,2),
∴M (0,2), ---2分
(2) ① 过点Q作QH ^ x轴,设垂足为H, 则HQ = y ,HP = x–t ,
由△HQP∽△OMC,得: , 即: t = x – 2y ,
, 即: t = x – 2y ,
∵ Q(x,y) 在y = 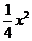 +1上, ∴ t = –
+1上, ∴ t = – + x –2. ---2分
+ x –2. ---2分
当点P与点C重合时,梯形不存在,此时,t = – 4,解得x = 1± ,
,
当Q与B或A重合时,四边形为平行四边形,此时,x = ± 2
∴x的取值范围是x ¹ 1± , 且x¹± 2的所有实数.
---2分
, 且x¹± 2的所有实数.
---2分
② 分两种情况讨论:
1)当CM > PQ时,则点P在线段OC上,
∵ CM∥PQ,CM = 2PQ ,
∴点M纵坐标为点Q纵坐标的2倍,即2
= 2(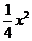 +1),解得x = 0 ,
+1),解得x = 0 ,
∴t = – + 0 –2 =
–2 .
---
2分
+ 0 –2 =
–2 .
---
2分
2)当CM < PQ时,则点P在OC的延长线上,
∵CM∥PQ,CM =  PQ,
PQ,
∴点Q纵坐标为点M纵坐标的2倍,即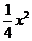 +1=2´2,解得: x = ±
+1=2´2,解得: x = ± .
---2分
.
---2分
当x = – 时,得t = –
时,得t = – –
– –2 = –8 –
–2 = –8 – ,
,
当x = 时, 得t =
时, 得t = –8.
---2分
–8.
---2分
23. (本小题满分10分)
(1) 作BH⊥PQ于点H, 在Rt△BHP中,
由条件知, PB = 320, ÐBPQ = 30°, 得 BH = 320sin30° = 160 < 200,
∴ 本次台风会影响B市. ---4分
(2) 如图, 若台风中心移动到P1时, 台风开始影响B市, 台风中心移动到P2时, 台风影响结束.
由(1)得BH = 160, 由条件得BP1=BP2 = 200,
∴所以P1P2 = 2 =240,
--- 4分
=240,
--- 4分
∴台风影响的时间t =  =
8(小时).
--- 2分
=
8(小时).
--- 2分
22. (本小题满分10分)
(1) ∵ BD∥AC,点B,A,E在同一条直线上, ∴ ÐDBA = ÐCAE,
又∵ 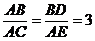 , ∴ △ABD∽△CAE.
--- 4分
, ∴ △ABD∽△CAE.
--- 4分
(2) ∵AB
= 3AC = 3BD,AD
=2 BD
,
BD
,
 (第22题) |
∴ AD2 + BD2 = 8BD2 + BD2 = 9BD2 =AB2,
∴ÐD =90°,
由(1)得 ÐE =ÐD = 90°,
∵ AE= BD
, EC =
BD
, EC = AD
=
AD
=
 BD , AB = 3BD
,
BD , AB = 3BD
,
∴在Rt△BCE中,BC2 = (AB + AE )2 + EC2
= (3BD + BD
)2 + (
BD
)2 + ( BD)2
=
BD)2
=  BD2
= 12a2 ,
BD2
= 12a2 ,
 (第23题) |
∴ BC = a .
--- 6分
a .
--- 6分
21. (本小题满分8分)
(1) 当a = 2, h = 3时,
V = a2h= 12 ;
S = 2a2+ 4ah =32 . --- 4分
(2) ∵a2h= 12, 2a(a + 2h) =32,
∴  , (a + 2h) =
, (a + 2h) = ,
,
∴ =
= =
= =
= . --- 4分
. --- 4分
20.45×184=3762.8(万人)
∴ 估计上海世博会参观的总人数约为3762.8万人. --- 1分
20. (本小题满分8分)
|

|
|
组别(万人) |
组中值(万人) |
频数 |
频率 |
|
7.5-14.5 |
11 |
5 |
0.25 |
|
14.5-21.5 |
18 |
6 |
0.30 |
|
21.5-28.5 |
25 |
6 |
0.30 |
|
28.5-35.5 |
32 |
3 |
0.15 |
填
频数分布表 --- 2分
频数分布直方图 --- 2分
(2)日参观人数不低于22万有9天, --- 1分
所占百分比为45%. --- 1分
(3)世博会前20天的平均每天参观人数约为
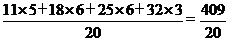 =20.45(万人) ---1分
=20.45(万人) ---1分
19. (本小题满分6分)
(1)命题n: 点(n , n2) 是直线y = nx与双曲线y = 的一个交点(
的一个交点( 是正整数). --- 3分
是正整数). --- 3分
(2)把 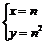 代入y = nx,左边= n2,右边= n·n = n2,
代入y = nx,左边= n2,右边= n·n = n2,
∵左边 =右边, ∴点(n,n2)在直线上. --- 2分
同理可证:点(n,n2)在双曲线上,
∴点(n,n2)是直线y = nx与双曲线y =  的一个交点,命题正确.
--- 1分
的一个交点,命题正确.
--- 1分
18. (本小题满分6分)
(1) 作图如右, 点 即为所求作的点;
--- 图形2分, 痕迹2分
即为所求作的点;
--- 图形2分, 痕迹2分
(2) 设AB的中垂线交AB于E,交x轴于F,
由作图可得,  ,
,  轴, 且OF =3,
轴, 且OF =3,
∵OP是坐标轴的角平分线,
∴ (3,3). --- 2分
(3,3). --- 2分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com