
3.已知⊙O的半径为5,弦AB的弦心距为3,则AB的长是( )
A.3 B.4 C.6 D.8
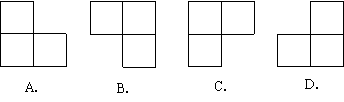
2. 如图,是由四个相同的小正方体组成的立体图形,它的俯视图是( )
如图,是由四个相同的小正方体组成的立体图形,它的俯视图是( )
 |
|||
|
|||
1.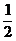 的相反数是(
)
的相反数是(
)
A.2 B.-2 C.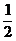 D.
D.
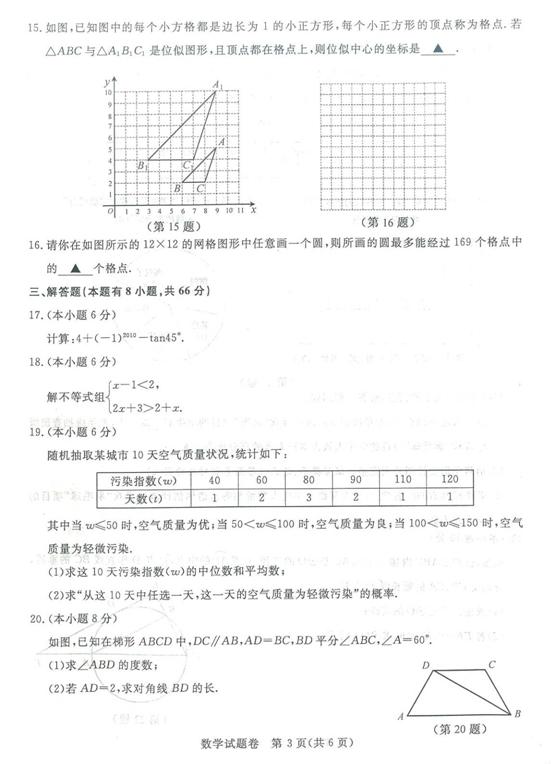
25.如图,已知在矩形ABCD中,AB=2,BC=3,P是线段AD边上的任意一点(不含端点A、D),连结PC, 过点P作PE⊥PC交AB于E
(1)在线段AD上是否存在不同于P的点Q,使得QC⊥QE?若存在,求线段AP与AQ之间的数量关系;若不存在,请说明理由;
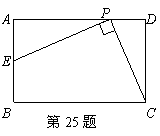 (2)当点P在AD上运动时,对应的点E也随之在AB上运动,求BE的取值范围.
(2)当点P在AD上运动时,对应的点E也随之在AB上运动,求BE的取值范围.






24.(本小题12分)如图,已知直角梯形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=AB=2,OC=3,过点B作BD⊥BC,交OA于点D.将∠DBC绕点B按顺时针方向旋转,角的两边分别交y轴的正半轴、x轴的正半轴于E和F.
(1)求经过A、B、C三点的抛物线的解析式;
(2)当BE经过(1)中抛物线的顶点时,求CF的长;
(3)连结EF,设△BEF与△BFC的面积之差为S,问:当CF为何值时S最小,并求出这个最小值.

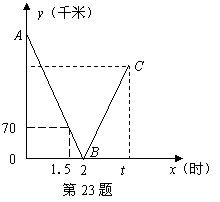
23.(本小题10分)一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶设行驶的时间为x(时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系
(1)根据图中信息,求线段AB所在直线的函数解析式和甲乙两地之间的距离;
(2)已知两车相遇时快车比慢车多行驶40千米,若快车从甲地到达乙地所需时间为t时,求t的值;
(3)若快车到达乙地后立刻返回甲地,慢车到达甲地后停止行驶,请你在图中画出快车从乙地返回到甲地过程中y关于x的函数的大致图象(温馨提示:请画在答题卷相对应的图上)
22. (本小题10分)如图,已知△ABC内接于⊙O,AC是⊙O的直径,D是的中点,过点D作直线BC的垂线,分别交CB、CA的延长线E、F
(本小题10分)如图,已知△ABC内接于⊙O,AC是⊙O的直径,D是的中点,过点D作直线BC的垂线,分别交CB、CA的延长线E、F
(1)求证:EF⊙是O的切线;
(2)若EF=8,EC=6,求⊙O的半径.
21.(本小题8分)某校欲举办“校园吉尼斯挑战赛”,为此该校在三个年级中各随机抽取一个班级进行了一次“你最喜欢的挑战项目”的问卷调查,每名学生都选了一项.已知被调查的三个年级的学生人数均为50人,根据收集到的数据,绘制成如下统计图表(不完整):


根据统计图表中的信息,解答下列问题:
(1)在本次随机调查中,七年级抽查班级中喜欢“跳绳”项目的学生有_________ 人,九年级抽查班级中喜欢“乒乓球”项目的学生人数占本班人数的百分比为_________;
(2)请将条形统计图补充完整;(温馨提示:请画在答题卷相对应的上)
(3)若该校共有900名学生(三个年级的学生人数都相等),请你估计该校喜欢“羽毛球”项目的学生总人数.
20.(本小题8分)如图,已知在梯形ABCD中,DC∥AB,AD=BC,BD平分∠ABC,∠A=60°.
 (1)求∠ABD的度数;
(1)求∠ABD的度数;
(2)若AD=2,求对角线BD的长.
19.(本小题6分)随机抽取某城市10天空气质量状况,统计如下:
|
污染指数(w) |
40 |
60 |
80 |
90 |
110 |
120 |
|
天数(t) |
1 |
2 |
3 |
2 |
1 |
1 |
其中当w≤50时,空气质量为优;当50<w≤100时,空气质量为良;当100<w≤150时,空气质量为轻微污染.
(1)求这10天污染指数(w)的中位数和平均数;
(2)求“从这10天任取一天,这一天空气质量为轻微污染”的概率
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com