
9. (2010年浙江宁波)如图1,有一张菱形纸片ABCD,
(2010年浙江宁波)如图1,有一张菱形纸片ABCD, ,
,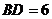 .
.
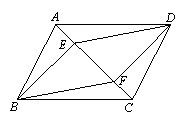
(1)请沿着AC剪一刀,把它分成两部分,把剪开的两部分拼成一个平行四
边形,在图2中用实数画出你所拼成的平行四边形;若沿着BD剪开,
请在图3中用实线画出拼成的平行四边形;并直接写出这两个平行四边
形的周长。
|
中用实线画出拼成的平行四边形。
(注:上述所画的平行四边形都不能与原菱形全等)



周长为__________ 周长为__________
|
[关键词]平行四边形
[答案]
解:(1)


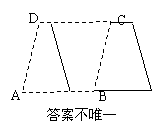
8.(2010年江苏宿迁)如图,在□ABCD中,点E、F是对角线AC上两点,且AE=CF.
 求证:∠EBF=∠FDE.
求证:∠EBF=∠FDE.
[关键词]平行四边形
[答案]
证明:连接BD交AC于O点 …… 1分
 ∵四边形ABCD是平行四边形
∵四边形ABCD是平行四边形
∴OA=OC,OB=OD ………………3分
又∵AE=CF
∴OE=OF
∴四边形BEDF是平行四边形 …… 6分
∴∠EBF=∠EDF …………… 8分
7.(2010年重庆市潼南县)如图,四边形ABCD是边长为2的正方形,点G是BC延长线上一点,连结AG,点E、F分别在AG上,连接BE、DF,∠1=∠2 , ∠3=∠4.
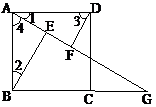 (1)证明:△ABE≌△DAF;
(1)证明:△ABE≌△DAF;
(2)若∠AGB=30°,求EF的长.
[关键词]全等三角形
[答案]解:(1)∵四边形ABCD是正方形
∴AB=AD
在△ABE和△DAF中

∴△ABE≌△DAF-----------------------4分
(2)∵四边形ABCD是正方形
∴∠1+∠4=900
∵∠3=∠4
∴∠1+∠3=900
∴∠AFD=900----------------------------6分
在正方形ABCD中, AD∥BC
∴∠1=∠AGB=300
在Rt△ADF中,∠AFD=900 AD=2
∴AF=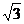 DF
=1----------------------------------------8分
DF
=1----------------------------------------8分
由(1)得△ABE≌△ADF
∴AE=DF=1
∴EF=AF-AE= -----------------------------------------10分
-----------------------------------------10分
7. (2010年贵州毕节地区)如图,已知: ABCD中,
(2010年贵州毕节地区)如图,已知: ABCD中,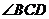 的平分线
的平分线 交边
交边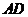 于
于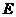 ,
, 的平分线
的平分线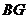 交
交 于
于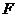 ,交
,交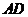 于
于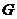 .求证:
.求证: .
.

[关键词]平行四边形、角平分线
[答案]证明:∵ 四边形 是平行四边形(已知),
是平行四边形(已知),
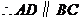 ,
,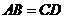 (平行四边形的对边平行,对边相等)
(平行四边形的对边平行,对边相等)
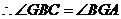 ,
,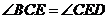 (两直线平行,内错角相等)
(两直线平行,内错角相等)
又∵ BG平分 ,
, 平分
平分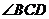 (已知)
(已知)
 ,
,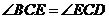 (角平分线定义)
(角平分线定义)
 ,
, .
.
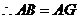 ,
,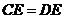 (在同一个三角形中,等角对等边)
(在同一个三角形中,等角对等边)
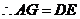
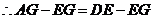 ,即
,即 . 分
. 分
6.(2010年福建晋江)如图,请在下列四个关系中,选出两个恰当的关系作为条件,推出四边形 是平行四边形,并予以证明.(写出一种即可)
是平行四边形,并予以证明.(写出一种即可)
 关系:①
关系:① ∥
∥ ,②
,② ,③
,③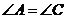 ,④
,④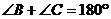 .
.
已知:在四边形 中, , ;
中, , ;
求证:四边形 是.
是.
[关键词]平行四边形的判定
[答案]已知:①③,①④,②④,③④均可,其余均不可以.
(解法一)
已知:在四边形 中,①
中,① ∥
∥ ,③
,③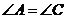 .……………………(2分)
.……………………(2分)
求证:四边形 是平行四边形.
是平行四边形.
证明:∵  ∥
∥
∴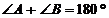 ,
,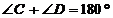
∵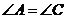 ,∴
,∴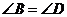
∴四边形 是平行四边形
是平行四边形
(解法二)
已知:在四边形 中,①
中,① ∥
∥ ,④
,④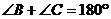 .
.
求证:四边形 是平行四边形.
是平行四边形.
证明:∵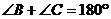 ,
,
∴ ∥
∥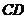
又∵ ∥
∥
∴四边形 是平行四边形.
是平行四边形.
(解法三)
已知:在四边形 中,②
中,② ,④
,④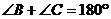 .
.
求证:四边形 是平行四边形.
是平行四边形.
证明:∵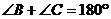 ,
,
∴ ∥
∥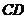 又
又
∵
∴四边形 是平行四边形.
是平行四边形.
(解法四)
已知:在四边形 中,③
中,③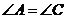 ,④
,④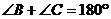 .
.
求证:四边形 是平行四边形.
是平行四边形.
证明:∵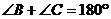 ,
,
∴ ∥
∥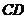
∴
又∵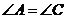
∴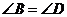
∴四边形 是平行四边形.
是平行四边形.
5.(2010年江苏泰州)如图,四边形ABCD是矩形,∠EDC=∠CAB,∠DEC=90°.
(1)求证:AC∥DE;
(2)过点B作BF⊥AC于点F,连结EF,试判断四边形BCEF的形状,并说明理由.

[答案]⑴在矩形ABCD中,AC∥DE,∴∠DCA=∠CAB,∵∠EDC=∠CAB,
∴∠DCA=∠EDC,∴AC∥DE;
⑵四边形BCEF是平行四边形.
理由:由∠DEC=90°,BF⊥AC,可得∠AFB=∠DEC=90°,
又∠EDC=∠CAB,AB=CD,
∴△DEC≌△AFB,∴DE=AF,由⑴得AC∥DE,
∴四边形AFED是平行四边形,∴AD∥EF且AD=EF,
∵在矩形ABCD中,AD∥BC且AD=BC,
∴EF∥BC且EF=BC,
∴四边形BCEF是平行四边形.
[关键词]矩形的性质 平行四边形的判定 全等三角形的判定
4. (2010年山东滨州)如图,四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.
(1)请判断四边形EFGH的形状?并说明为什么.
(2)若使四边形EFGH为正方形,那么四边形ABCD的对角线应具有怎样的性质?
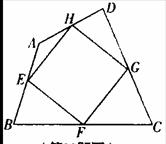
解:(1) 四边形EFGH为平行四边形,连接AC
∵E、F分别是AB、BC的中点,EF∥AC,EF=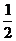 AC.
AC.
同理HG∥AC,HG=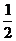 AC.
AC.
∴EF∥HG, EF=HG.
∴四边形EFGH是平行四边形
(2) 四边形ABCD的对角线垂直且相等.
3.(2010浙江省嘉兴)如图,在□ABCD中,已知点E在AB上,点F在CD上且AE=CF.
(1)求证:DE=BF;(2)连结BD,并写出图中所有的全等三角形.(不要求证明)
 [关键词]平行四边形的判定与性质、全等三角形
[关键词]平行四边形的判定与性质、全等三角形
[答案](1)在□ABCD中,AB//CD,AB=CD.
∵AE=CF,∴BE=DF,且BE//DF.
∴四边形BFDE是平行四边形.
∴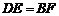 . …5分
. …5分
 (2)连结BD,如图,
(2)连结BD,如图,
图中有三对全等三角形:
△ADE≌△CBF,
△BDE≌△DBF,
△ABD≌△CDB. …3分
2. (2010年浙江衢州)已知:如图,E,F分别是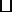 ABCD的边AD,BC的中点.
ABCD的边AD,BC的中点.
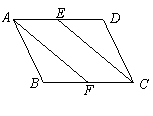 求证:AF=CE.
求证:AF=CE.
证明:方法1:
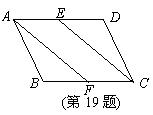 ∵ 四边形ABCD是平行四边形,且E,F分别是AD,BC的中点,∴ AE = CF. ……2分
∵ 四边形ABCD是平行四边形,且E,F分别是AD,BC的中点,∴ AE = CF. ……2分
又 ∵ 四边形ABCD是平行四边形,
∴ AD∥BC,即AE∥CF.
∴ 四边形AFCE是平行四边形. ……3分
∴ AF=CE. ……1分
方法2:
∵ 四边形ABCD是平行四边形,且E,F分别是AD,BC的中点,
∴ BF=DE. ……2分
又 ∵ 四边形ABCD是平行四边形,
∴ ∠B=∠D,AB=CD.
∴ △ABF≌△CDE. ……3分
∴ AF=CE. ……1分
1.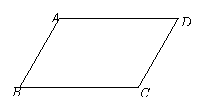 (2010年福建晋江)如图,请在下列四个关系中,选出两个恰当的关系作为条件,推出四边形
(2010年福建晋江)如图,请在下列四个关系中,选出两个恰当的关系作为条件,推出四边形 是平行四边形,并予以证明.(写出一种即可)
是平行四边形,并予以证明.(写出一种即可)
关系:① ∥
∥ ,②
,② ,③
,③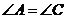 ,④
,④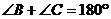 .
.
已知:在四边形 中, , ;
中, , ;
求证:四边形 是平行四边形.
是平行四边形.
解:已知:①③,①④,②④,③④均可,其余均不可以.
(解法一)
已知:在四边形 中,①
中,① ∥
∥ ,③
,③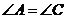 .……………………(2分)
.……………………(2分)
求证:四边形 是平行四边形.
是平行四边形.
证明:∵  ∥
∥
∴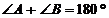 ,
,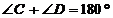 ………………………………………(5分)
………………………………………(5分)
∵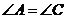 ,∴
,∴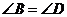
∴四边形 是平行四边形…………………………………………………(8分)
是平行四边形…………………………………………………(8分)
(解法二)
已知:在四边形 中,①
中,① ∥
∥ ,④
,④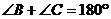 .………………(2分)
.………………(2分)
求证:四边形 是平行四边形.
是平行四边形.
证明:∵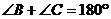 ,
,
∴ ∥
∥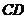 ……………………………………………………………………(5分)
……………………………………………………………………(5分)
又∵ ∥
∥
∴四边形 是平行四边形.…………………………………………………(8分)
是平行四边形.…………………………………………………(8分)
(解法三)
已知:在四边形 中,②
中,② ,④
,④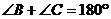 .………………(2分)
.………………(2分)
求证:四边形 是平行四边形.
是平行四边形.
证明:∵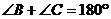 ,
,
∴ ∥
∥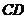 ……………………………………………………………………(5分)
……………………………………………………………………(5分)
又∵
∴四边形 是平行四边形.…………………………………………………(8分)
是平行四边形.…………………………………………………(8分)
(解法四)
已知:在四边形 中,③
中,③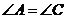 ,④
,④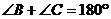 .………………(2分)
.………………(2分)
求证:四边形 是平行四边形.
是平行四边形.
证明:∵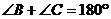 ,
,
∴ ∥
∥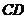 ……………………………………………………………………(4分)
……………………………………………………………………(4分)
∴ ………………………………………………………………(6分)
………………………………………………………………(6分)
又∵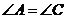
∴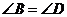
∴四边形 是平行四边形.…………………………………………………(8分)
是平行四边形.…………………………………………………(8分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com