2．某个命题与正整数n有关，如果当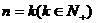时命题成立，那么可推得当时命题也成立. 现已知当时该命题不成立，那么可推得　 (　 )

　　　 A．当n=6时该命题不成立　　　　　　　　　　　 B．当n=6时该命题成立

　　　 C．当n=4时该命题不成立　　　　　　　　　　　 D．当n=4时该命题成立

1．用数学归纳法证明

时，由n=k的假设到证明n=k+1时，等式左边应添加的式子是　　　　 (　 )

　　　 A．　　　 B．　 C．　 D．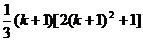

3．数学归纳法的应用:证明等式、不等式、整除性；探求平面几何及数列问题；

2.数学归纳法:对于与正整数有关的命题证明：

①当n=n₀(每第一个值)时成立；

②假设n=k(k≥n₀)时命题成立，证明当n=k+1时命题成立；

这就证明了命题对n₀以后的所有正整数都成立。

(1)事实上:第一步证明了“归纳基础”；第二步证明了“递推规律”--“若n=k命题成立，则n=k+1命题成立”，从而可以无限的递推下去，保证了对n₀以后的所有正整数都成立。

(2)两点注意: ①两步缺一不可(如命题2)

②证“n=k+1成立”必用“n=k成立”(归纳假设)

如对于等式2+4+……2n=n²+n+1可以证明“假设n=k时成立，则n=k+1时也成立”，没有归纳基础。事实上这个等式是不成立的。

1.归纳法: 由特殊事例推出一般结论的推理方法.有不完全归纳法,完全归纳法.

2.能用数学归纳法证明恒等式、不等式、整除性；探求平面几何及数列问题；

1.理解数学归纳法的原理; 掌握数学归纳法的证明步骤;

现在越来越多的中学生使用词典，有人选择使用传统词典，有人则喜欢使用电子词典。请你以“Printed dictionary or E-dictionary, which do you prefer?”为题，按照下列要点写一篇英语短文，可根据需要适当发挥：

1、传统词典：内容详、例句多… 缺点：携带不便…

2、电子词典：省时、方便… 缺点：例句少…

3、我选用的词典及理由

注意：1、词数：100-120 文章题目和开头已给出(不计入词数)。

　　 　　　2、参考词汇：电子词典 e-dictionary　 传统词典　 printed dictionary　

条目 entry　　　　 释义　 definition