
3.用数学归纳法证明“1+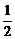 +
+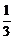 +…+
+…+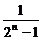 <n(n∈N*,n>1)”时,由n=k(k>1)不等式成立,推证n=k+1时,左边应增加的项数是 ( )
<n(n∈N*,n>1)”时,由n=k(k>1)不等式成立,推证n=k+1时,左边应增加的项数是 ( )
A.2k-1 B.2k-1 C.2k D.2k+1
[填空题]
2.凸n边形有f(n)条对角线,则凸n+1边形有对角线条数f(n+1)为 ( )
A.f(n)+n+1 B.f(n)+n C.f(n)+n-1 D.f(n)+n-2
1.设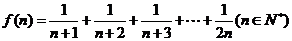 ,则
,则 ( )
( )
A.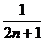 B.
B.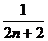 C.
C. D.
D.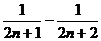
2.题型.方法.思想:证明恒等式、不等式、整除性;探求平面几何及数列问题;
证明的关键是”找出n与n+1的递推关系,用好归纳假设,凑出结论”
同步练习 3.1数学归纳法
[选择题]
1.数学归纳法的步骤、原理、注意事项:
[例1]用数学归纳法证明等式:
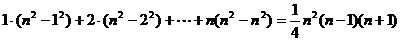 .
.
[证明]
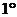 . 当
. 当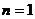 时,左边
时,左边 ,右边
,右边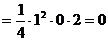 ,∴左边=右边,
,∴左边=右边,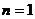 时等式成立;
时等式成立;
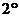 . 假设
. 假设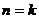 时等式成立,即
时等式成立,即
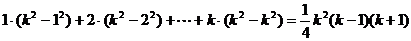 ,
,
∴当 时,左边
时,左边
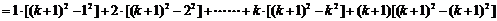
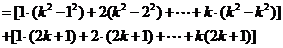
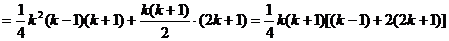
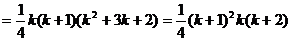 =右边,即
=右边,即 时等式成立,
时等式成立,
根据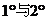 ,等式对
,等式对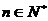 都正确.
都正确.
[例2]是否存在正整数m,使得f(n)=(2n+7)·3n+9对任意正整数n都能被m整除?若存在,求出最大的m值,并证明你的结论;若不存在,请说明理由.
解:由f(n)=(2n+7)·3n+9,得f(1)=36, f(2)=3×36, f(3)=10×36, f(4)=34×36,由此猜想m=36.
下面用数学归纳法证明:
(1)当n=1时,显然成立.
(2)假设n=k时, f(k)能被36整除,即f(k)=(2k+7)·3k+9能被36整除;当n=k+1时,[2(k+1)+7]·3k+1+9=3[(2k+7)·3k+9]+18(3k-1-1),
由于3k-1-1是2的倍数,故18(3k-1-1)能被36整除.这就是说,当n=k+1时,f(n)也能被36整除.
由(1)(2)可知对一切正整数n都有f(n)=(2n+7)·3n+9能被36整除,m的最大值为36.
方法提炼:本题是探索性命题,它通过观察、归纳、特殊化猜想出结论,再用数学归纳法证明。
[例3]已知y=f(x)满足f(n-1)=f(n)-lgan-1(n≥2,n∈N)且f(1)=-lga,是否存在实数α、β使f(n)=(αn2+βn-1)lga对任何n∈N *都成立,证明你的结论.
解:∵f(n)=f(n-1)+lgan-1,令n=2,则f(2)=f(1)+f(a)=-lga+lga=0.
又f(1)=-lga,
∴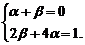 ∴
∴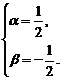 ∴f(n)=(
∴f(n)=(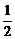 n2-
n2-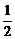 n-1)lga.
n-1)lga.
证明:(1)当n=1时,显然成立.
(2)假设n=k时成立,即f(k)=(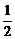 k2-
k2-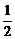 k-1)lga,
k-1)lga,
则n=k+1时,f(k+1)=f(k)+lgak=f(k)+klga=(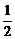 k2-
k2-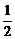 k-1+k)lga=[
k-1+k)lga=[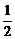 (k+1)2-
(k+1)2-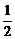 (k+1)-1]lga.
(k+1)-1]lga.
∴当n=k+1时,等式成立.
综合(1)(2)可知,存在实数α、β且α=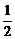 ,β=-
,β=-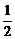 ,使f(n)=(αn2+βn-1)lga对任意n∈N*都成立.
,使f(n)=(αn2+βn-1)lga对任意n∈N*都成立.
解题回顾:本题与例2同是探索性命题,取n=2求出α、β,再证明一般性。
[例4](2006江西)已知数列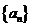 满足:
满足: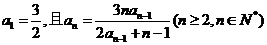 .
.
(1) 求数列{an}的通项公式;
(2) 证明:对一切正整数n,不等式a1.a2.……an<2.n! 恒成立.
解: (1)将条件变为: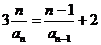 ,
,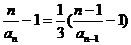 ,因此,
,因此, 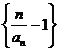 为一个等比数列.
为一个等比数列.
其首项为 ,公比为
,公比为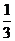 ,从而
,从而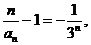
据此得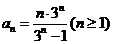 .
.
(2)证:据①得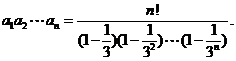 为证
为证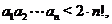
只要证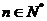 时有
时有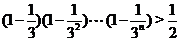 .…………②
.…………②
显然,左端每个因式皆为正数,先证明,对每个n∈N*
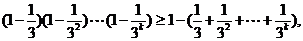 …………③
…………③
用数学归纳法证明③式:
10当n=1时,显然③式成立,
20设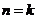 时,③式成立
时,③式成立
即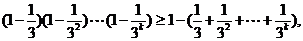 记此式为f(k)≥g(k)……④
记此式为f(k)≥g(k)……④
则当n=k+1时,只需证
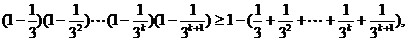
即 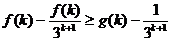 代④知只需证:f(k)≤1.此式显然成立。
代④知只需证:f(k)≤1.此式显然成立。
∴n=k+1时,不等式成立。由归纳原理知,不等式对任意正整数n都成立。
拓展发散:题(1)对递推公式变形后,整体代换把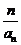 看成一个数列,处理得好.
看成一个数列,处理得好.
若用“猜想+证明”的方法求通项公式,就有点难。
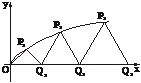
[研讨.欣赏]如下图,设P1,P2,P3,…,Pn,…是曲线y=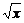 上的点列,Q1,Q2,Q3, …,Qn,…是x轴正半轴上的点列,且△OQ1P1,△Q1Q2P2,…,△Qn-1QnPn,…都是正三角形,设它们的边长为a1,a2,…,an,…,求证:a1+a2+…+an=
上的点列,Q1,Q2,Q3, …,Qn,…是x轴正半轴上的点列,且△OQ1P1,△Q1Q2P2,…,△Qn-1QnPn,…都是正三角形,设它们的边长为a1,a2,…,an,…,求证:a1+a2+…+an=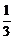 n(n+1).
n(n+1).
证明:(1)当n=1时,点P1是直线y=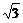 x与曲线y=
x与曲线y=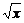 的交点,
的交点,
∴可求出P1(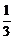 ,
,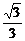 ).
).
∴a1=|OP1|=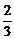 .而
.而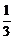 ×1×2=
×1×2=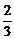 ,命题成立.
,命题成立.
(2)假设n=k(k∈N*)时命题成立,即a1+a2+…+ak=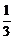 k(k+1),则点Qk的坐标为(
k(k+1),则点Qk的坐标为(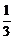 k(k+1),0),
k(k+1),0),
∴直线QkPk+1的方程为y=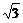 [x-
[x-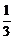 k(k+1)].代入y=
k(k+1)].代入y=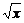 ,解得Pk+1点的坐标为
,解得Pk+1点的坐标为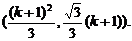
∴ak+1=|QkPk+1|=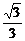 (k+1)·
(k+1)·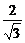 =
=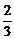 (k+1).
(k+1).
∴a1+a2+…+ak+a k+1=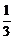 k(k+1)+
k(k+1)+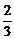 (k+1)=
(k+1)=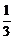 (k+1)(k+2).
(k+1)(k+2).
∴当n=k+1时,命题成立.
由(1)(2)可知,命题对所有正整数都成立.
解法点评:
本题的关键是求出Pk+1的纵坐标,再根据正三角形高与边的关系求出|QkP k+1|.
6.如图,第n个图形是由正n+2边形“扩展”而来(n=1,2,3,…),则第n-2个图形中共有____________个顶点.

简答:1-4.BCBD; 5. 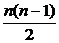 ; 6. 观察规律…第n-2个图形有(n+2-2)2+(n+2-2)=n2+n个顶点
; 6. 观察规律…第n-2个图形有(n+2-2)2+(n+2-2)=n2+n个顶点
5.平面内有n(n≥2)条直线,其中任何两条不平行,任何三条不过同一点,猜想这n条直线交点的个数为 .
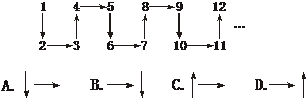
4.(2004太原模拟)若把正整数按下图所示的规律排序,则从2002到2004年的箭头方向依次为 ( )
3.用数学归纳法证明对n为正偶数时某命题成立,若已假设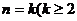 为偶数)时命题为真,则还需要用归纳假设再证
( )
为偶数)时命题为真,则还需要用归纳假设再证
( )
A. 时等式成立 B.
时等式成立 B.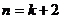 时等式成立
时等式成立
C.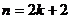 时等式成立 D.
时等式成立 D.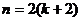 时等式成立
时等式成立
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com