
2、对“流星雨的出现与彗星有十分密切的关系”一句解说有误的一项是( )
A、 流星雨是由彗星的颗粒尘埃构成的
B、 流星雨在形成以前绕太阳运动,彗星也绕太阳运动
C、 流星雨在形成以前处在彗星的轨道及附近区域
D、流星雨在形成以前同彗星一起绕太阳运动
1、根据文意,对“流星雨”表述恰当的一项是( )
A、几颗乃至成千上万颗流星像节日的礼花从天空中某一辐射点迸发出来的现象叫流星雨。
B、星中与冰相似的物质脱离彗星后,几颗或者成千上万颗地从天空中某一辐射点迸发出来的现象叫流星雨。
C、彗星的内部喷发,从彗星上喷出来的尘埃颗粒,有时几颗,有时成千上万颗地从天空中某一辐射点有周期地穿过大气层,迸发出来形成的星空奇观叫流星雨。
D、星的内部喷发,从彗星上喷发出来的尘埃颗粒,几颗或者成千上万颗,有周期地从天空中某一辐射点迸发出来,穿过大气层后形成的星空奇观叫流星雨。
10.是否存在常数a,b使等式
1·n+2(n-1)+3(n-2)+…+(n-2)·3+(n-1)·2+n·1=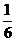 n(n+a)(n+b)对一切自然数N都成立,并证明你的结论.
n(n+a)(n+b)对一切自然数N都成立,并证明你的结论.
解:令n=1,得 1=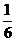 (1+a)(1+b),
(1+a)(1+b),
令n=2,得 4=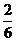 (2+a)(2+b),
(2+a)(2+b),
整理得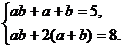 解得a=1,b=2.
解得a=1,b=2.
下面用数学归纳法证明等式:
1·n+2·(n-1)+3·(n-2)+…+(n-1)·2+n·1
=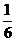 n(n+1)(n+2).
n(n+1)(n+2).
(1)当n=1时,1=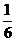 ·1·2·3,结论成立.
·1·2·3,结论成立.
(2)假设n=k时结论成立,即
1·k+2·(k-1)+3·(k-2)+…+(k-1)·2+k·1
=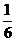 k(k+1)(k+2).
k(k+1)(k+2).
当n=k+1时,则
1·(k+1)+2·k+3·(k-1)+…+(k-1)·3+k·3+(k+1)·1
=1·k+2·(k-1)+3·(k-2)+…+(k-2)·3+(k-1)·2+k·1+(1+2+3+…+(k-1)+k+(k+1))
=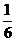 k(k+1)(k+2)+
k(k+1)(k+2)+ 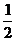 (k+1)(k+2)
(k+1)(k+2)
=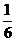 (k+1)(k+2)(k+3)
(k+1)(k+2)(k+3)
说明当n=k+1时结论也成立.
综合上述,可知结论对一切n∈N都成立.
[探索题]已知数列{bn}是等差数列,b1=1,b1+b2+…+b10=100.
(1)求数列{bn}的通项公式bn;
(2)设数列{an}的通项an=lg(1+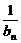 ),记Sn为{an}的前n项和,试比较Sn与
),记Sn为{an}的前n项和,试比较Sn与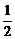 lgbn+1的大小,并证明你的结论.
lgbn+1的大小,并证明你的结论.
解:(1)容易得bn=2n-1.
(2)由bn=2n-1,
知Sn=lg(1+1)+1g(1+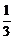 )+…+lg(1+
)+…+lg(1+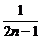 )=lg(1+1)(1+
)=lg(1+1)(1+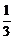 )·…·(1+
)·…·(1+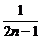 ). 又
). 又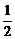 1gbn+1=1g
1gbn+1=1g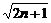 ,
,
因此要比较Sn与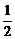 1gbn+1的大小,可先比较(1+1)(1+
1gbn+1的大小,可先比较(1+1)(1+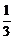 )·…·(1+
)·…·(1+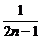 )与
)与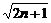 的大小. 取n=1,2,3可以发现:前者大于后者,由此推测
的大小. 取n=1,2,3可以发现:前者大于后者,由此推测
(1+1)(1+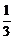 )· …· (1+
)· …· (1+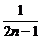 )>
)>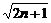 .
①
.
①
下面用数学归纳法证明上面猜想:
当n=1时,不等式①成立.
假设n=k时,不等式①成立,即
(1+1)(1+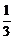 )·…·(1+
)·…·(1+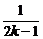 )>
)>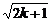 .
.
那么n=k+1时,
(1+1)(1+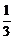 )·…·(1+
)·…·(1+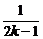 )(1+
)(1+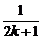 )>
)>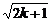 (1+
(1+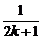 )
)
=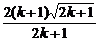 . 又[
. 又[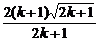 ]2-(
]2-(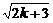 )2=
)2=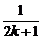 >0,
>0,
∴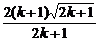 >
>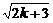 =
=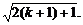
∴当n=k+1时①成立.
综上所述,n∈N*时①成立.
由函数单调性可判定Sn>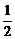 1gbn+1.
1gbn+1.
9.已知数列{an}中,a1=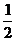 ,Sn=n2·an (n∈N)
,Sn=n2·an (n∈N)
(Ⅰ)求a2,a3,a4的值;
(Ⅱ)推测数列{an}的通项公式,并用数学归纳法加以证明;
解:(Ⅰ)a1=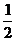 , ∵S2=4a2,即
, ∵S2=4a2,即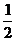 +a2=4a2,
+a2=4a2,
∴ a2=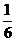 ;
;
∵ S3=9a3,即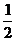 +
+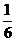 +a3=9a3, ∴ a3=
+a3=9a3, ∴ a3=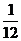 ;
;
∵ S4=16a4,即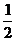 +
+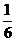 +
+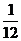 +a4=16a4,
+a4=16a4,
∴ a4=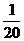 ,
,
(Ⅱ)猜想an=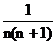 .证明如下:
.证明如下:
当n=1时,a1=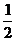 =
=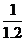 ,结论成立.
,结论成立.
假设n=k时成立,即ak=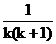 .
.
即 Sk=a1+a2+a3+…+ak=1- =
=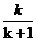 .
.
由 Sk+1=(k+1)2·ak+1,即Sk+ak+1=(k+1)2ak+1,
得 ak+1=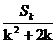 =
=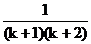 ,
,
说明当n=k+1时,结论也成立.
综合上述,可知对一切n∈N,都有an=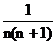 .
.
法二: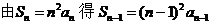 ,
,
相减得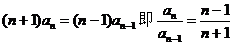 ,
,
连乘法可得: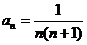
8.(2004重庆)设数列{an}满足a1=2,an+1=an+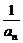 (n=1,2,…).
(n=1,2,…).
(1)证明an>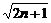 对一切正整数n都成立;
对一切正整数n都成立;
(2)令bn=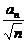 (n=1,2,…),判定bn与bn+1的大小,并说明理由.
(n=1,2,…),判定bn与bn+1的大小,并说明理由.
(1)证法一:当n=1时,a1=2>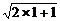 ,不等式成立.
,不等式成立.
假设n=k时,ak>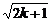 成立,
成立,
当n=k+1时,ak+12=ak2+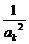 +2>2k+3+
+2>2k+3+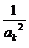 >2(k+1)+1,
>2(k+1)+1,
∴当n=k+1时,ak+1>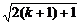 成立.
成立.
综上,由数学归纳法可知,an>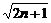 对一切正整数成立.
对一切正整数成立.
证法二:当n=1时,a1=2>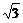 =
=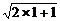 结论成立.
结论成立.
假设n=k时结论成立,即ak>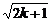 ,
,
当n=k+1时,由函数f(x)=x+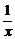 (x>1)的单调递增性和归纳假设有
(x>1)的单调递增性和归纳假设有
ak+1=ak+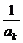 >
>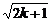 +
+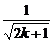 =
=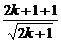 =
= =
=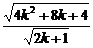 >
>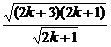 =
=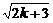 .
.
∴当n=k+1时,结论成立.
因此,an>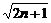 对一切正整数n均成立.
对一切正整数n均成立.
(2)解: =
=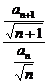 =(1+
=(1+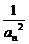 )
)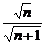 <(1+
<(1+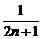 )
)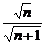 =
=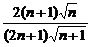 =
=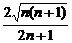 =
=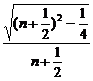 <1.
<1.
故bn+1<bn.
7.用数学归纳法证明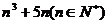 能被6 整除.
能被6 整除.
[证明]
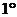 . 当
. 当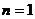 时,13+5×1=6能被6整除,命题正确;
时,13+5×1=6能被6整除,命题正确;
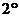 . 假设
. 假设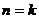 时命题正确,即
时命题正确,即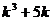 能被6整除,
能被6整除,
∴当 时,
时,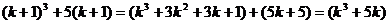
 ,
,
∵两个连续的整数的乘积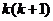 是偶数,
是偶数,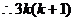 能被6整除,
能被6整除,
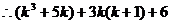 能被6整除,即当
能被6整除,即当 时命题也正确,
时命题也正确,
由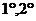 知命题时
知命题时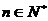 都正确.
都正确.
6. Sn=(2n-1)2 答4;
[解答题]
6.观察下表,设第n行的各数之和为Sn,则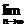
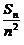 =__________.
=__________.
1
2 3 4
3 4 5 6 7
4 5 6 7 8 9 10
……
简答.提示:1-3.DCC; 4. .2(2k+1);5.(1) 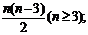 (2) n2-n-1;
(2) n2-n-1;
5.由归纳原理分别探求:
(1)凸n边形的对角线条数f(n)= ;
(2)平面内n个圆,其中每两个圆都相交于两点,且任意三个圆不相交于同一点,则该n个圆分平面区域数f(n)= .
4.用数学归纳法证明“(n+1)(n+2)·…·(n+n)=2n·1·3·…·(2n-1)”,从“k到k+1”左端需增乘的代数式为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com