
8. 函数y=中,自变量x的取值范围是__________.
7. -2的绝对值的结果是__________.
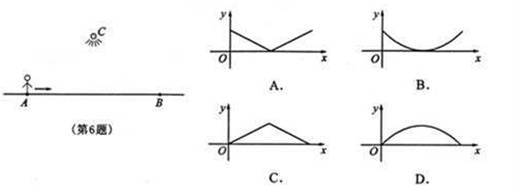
6.,如图,夜晚,小亮从点A经过路灯C的正下方沿直线走到点B,他的影长y随他与点A之间的距离x的变化而变化,那么表示y与x之间的函数关系的图象大致为
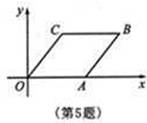
5.如图,在平面直角坐标系中,菱形OABC的顶点C的坐标是(3,4),则顶点A、B的坐标分别是
A.(4,0)、(7,4) B.(5,0)、(8,4) C.(4,0)、(7,4) D.(5,0)、(8,4)
4.甲各蔬菜保鲜适宜的温度是1℃-5℃,乙种蔬菜保鲜适宜的温度是3℃-8℃,将这两种蔬菜放在一起同时保鲜,适宜的温度是
A.1℃-3℃ B.3℃-5℃ C.5℃-8℃ D.1℃-8℃
3.如图,下列各数中,数轴点A表示的可能是
A.4的算术平方根 B.4的立方根 C.8的算术平方根 D.8的立方根
2.计算a3·a4的结果是
A.a6 B.a7 C.a8 D.a12
1.-3的倒数是
 A.-3 B.3
C.-
D.
A.-3 B.3
C.-
D.
(19)(本小题6分)
解不等式组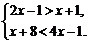
(20)(本小题8分)
已知反比例函数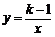 (
(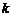 为常数,
为常数, ).
).
(Ⅰ)若点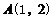 在这个函数的图象上,求
在这个函数的图象上,求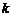 的值;
的值;
(Ⅱ)若在这个函数图象的每一支上,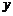 随
随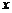 的增大而减小,求
的增大而减小,求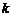 的取值范围;
的取值范围;
(Ⅲ)若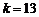 ,试判断点
,试判断点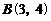 ,
,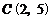 是否在这个函数的图象上,并说明理由.
是否在这个函数的图象上,并说明理由.
(21)(本小题8分)
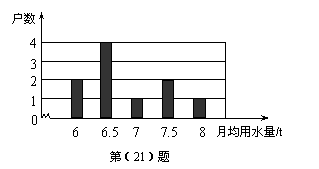 我国是世界上严重缺水的国家之一.为了倡导“节约用水从我做起”,小刚在他所在班的50名同学中,随机调查了10名同学家庭中一年的月均用水量(单位:t),并将调查结果绘成了如下的条形统计图.
我国是世界上严重缺水的国家之一.为了倡导“节约用水从我做起”,小刚在他所在班的50名同学中,随机调查了10名同学家庭中一年的月均用水量(单位:t),并将调查结果绘成了如下的条形统计图.
(Ⅰ)求这10个样本数据的平均数、众数和中位数;
(Ⅱ)根据样本数据,估计小刚所在班50名同学家庭中月均用水量不超过7 t的约有多少户.
(22)(本小题8分)
已知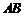 是⊙
是⊙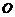 的直径,
的直径,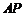 是⊙
是⊙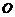 的切线,
的切线,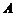 是切点,
是切点,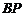 与⊙
与⊙ 交于点
交于点 .
.
(Ⅰ)如图①,若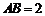 ,
,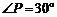 ,求
,求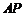 的长(结果保留根号);
的长(结果保留根号);
 (Ⅱ)如图②,若
(Ⅱ)如图②,若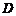 为
为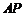 的中点,求证直线
的中点,求证直线 是⊙
是⊙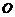 的切线.
的切线.
(23)(本小题8分)
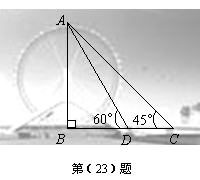 永乐桥摩天轮是天津市的标志性景观之一.某校数学兴趣小组要测量摩天轮的高度.如图,他们在C处测得摩天轮的最高点A的仰角为
永乐桥摩天轮是天津市的标志性景观之一.某校数学兴趣小组要测量摩天轮的高度.如图,他们在C处测得摩天轮的最高点A的仰角为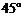 ,再往摩天轮的方向前进50 m至D处,测得最高点A的仰角为
,再往摩天轮的方向前进50 m至D处,测得最高点A的仰角为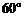 .
.
求该兴趣小组测得的摩天轮的高度AB(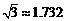 ,
,
结果保留整数).
(24)(本小题8分)
注意:为了使同学们更好地解答本题,我们提供了一种解题思路,你可以依照这个思路按下面的要求填空,完成本题的解答.也可以选用其他的解题方案,此时不必填空,只需按照解答题的一般要求进行解答.
青山村种的水稻2007年平均每公顷产8 000 kg,2009年平均每公顷产9 680 kg,求该村水稻每公顷产量的年平均增长率.
解题方案:
设该村水稻每公顷产量的年平均增长率为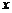 .
.
(Ⅰ)用含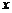 的代数式表示:
的代数式表示:
① 2008年种的水稻平均每公顷的产量为 ;
② 2009年种的水稻平均每公顷的产量为 ;
(Ⅱ)根据题意,列出相应方程 ;
(Ⅲ)解这个方程,得 ;
(Ⅳ)检验: ;
(Ⅴ)答:该村水稻每公顷产量的年平均增长率为 %.
(25)(本小题10分)
在平面直角坐标系中,矩形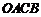 的顶点O在坐标原点,顶点A、B分别在
的顶点O在坐标原点,顶点A、B分别在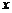 轴、
轴、
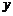 轴的正半轴上,
轴的正半轴上,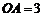 ,
,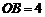 ,D为边OB的中点.
,D为边OB的中点.
 (Ⅰ)若
(Ⅰ)若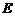 为边
为边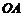 上的一个动点,当△
上的一个动点,当△ 的周长最小时,求点
的周长最小时,求点 的坐标;
的坐标;
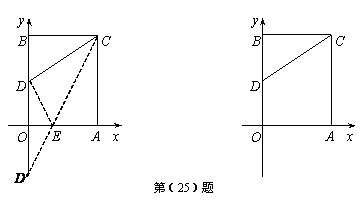
(Ⅱ)若 、
、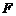 为边
为边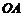 上的两个动点,且
上的两个动点,且 ,当四边形
,当四边形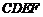 的周长最小时,求点
的周长最小时,求点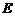 、
、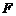 的坐标.
的坐标.
(26)(本小题10分)
在平面直角坐标系中,已知抛物线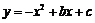 与
与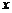 轴交于点
轴交于点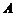 、
、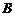 (点
(点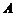 在点
在点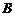 的左侧),与
的左侧),与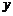 轴的正半轴交于点
轴的正半轴交于点 ,顶点为
,顶点为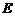 .
.
(Ⅰ)若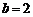 ,
,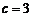 ,求此时抛物线顶点
,求此时抛物线顶点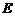 的坐标;
的坐标;
(Ⅱ)将(Ⅰ)中的抛物线向下平移,若平移后,在四边形ABEC中满足
S△BCE = S△ABC,求此时直线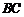 的解析式;
的解析式;
(Ⅲ)将(Ⅰ)中的抛物线作适当的平移,若平移后,在四边形ABEC中满足
S△BCE = 2S△AOC,且顶点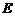 恰好落在直线
恰好落在直线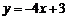 上,求此时抛物线的解析式.
上,求此时抛物线的解析式.
 (11)若
(11)若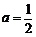 ,则
,则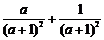 的值为
.
的值为
.
(12)已知一次函数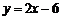 与
与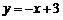 的图象交于点
的图象交于点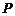 ,
,
则点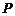 的坐标为
.
的坐标为
.
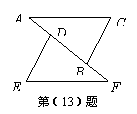
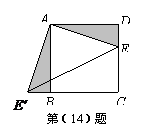 (13)如图,已知
(13)如图,已知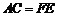 ,
,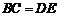 ,点A、D、B、F在一
,点A、D、B、F在一
条直线上,要使△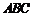 ≌△
≌△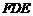 ,还需添加一个条件,
,还需添加一个条件,
这个条件可以是 .
(14)如图,已知正方形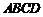 的边长为3,
的边长为3,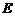 为
为 边上一点,
边上一点,
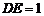 .以点
.以点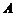 为中心,把△
为中心,把△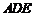 顺时针旋转
顺时针旋转 ,得
,得
△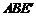 ,连接
,连接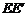 ,则
,则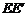 的长等于
.
的长等于
.
(15)甲盒装有3个乒乓球,分别标号为1,2,3;乙盒装有2个乒乓球,分别标号为
1,2.现分别从每个盒中随机地取出1个球,则取出的两球标号之和为4的概率是 .
(16)已知二次函数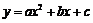 (
(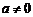 )中自变量
)中自变量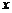 和函数值
和函数值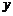 的部分对应值如下表:
的部分对应值如下表:
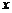 |
… |
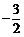 |
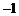 |
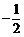 |
0 |
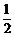 |
1 |
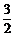 |
… |
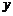 |
… |
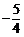 |
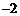 |
 |
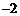 |
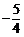 |
0 |
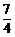 |
… |
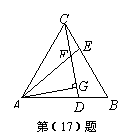 则该二次函数的解析式为
.
则该二次函数的解析式为
.
(17)如图,等边三角形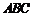 中,
中,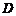 、
、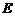 分别为
分别为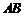 、
、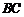 边上
边上
的点,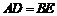 ,
,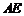 与
与 交于点
交于点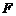 ,
,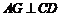 于点
于点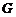 ,
,
则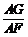 的值为
.
的值为
.
(18)有一张矩形纸片ABCD,按下面步骤进行折叠:
第一步:如图①,将矩形纸片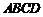 折叠,使点B、D重合,点C落在点
折叠,使点B、D重合,点C落在点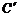 处,得折痕EF;
处,得折痕EF;
第二步:如图②,将五边形 折叠,使AE、
折叠,使AE、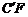 重合,得折痕DG,再打开;
重合,得折痕DG,再打开;
第三步:如图③,进一步折叠,使AE、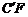 均落在DG上,点A、
均落在DG上,点A、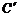 落在点
落在点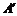 处,点E、F落在点
处,点E、F落在点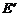 处,得折痕MN、QP.
处,得折痕MN、QP.
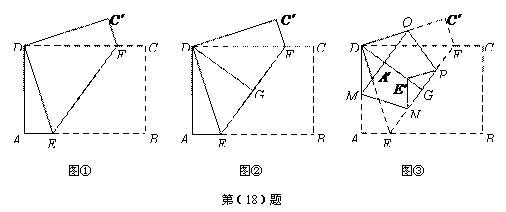 这样,就可以折出一个五边形
这样,就可以折出一个五边形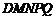 .
.
(Ⅰ)请写出图①中一组相等的线段 (写出一组即可);
(Ⅱ)若这样折出的五边形DMNPQ(如图③)恰好是一个正五边形,当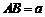 ,
,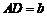 ,
,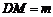 时,有下列结论:
时,有下列结论:
①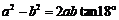 ; ②
; ②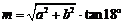 ;
;
③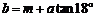 ; ④
; ④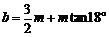 .
.
其中,正确结论的序号是 (把你认为正确结论的序号都填上).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com