7．在等边三角形、正方形、菱形和等腰梯形这四个图形中，是中心对称图形的个数为()

A．1个　　　 B．2个　　　　 C．3个　　　　 D．4个

6．一组数据3，4，x，6，8的平均数是5，则这组数据的中位数是()

A．4　　 B．5　　 C．6　　　　 D．7

5．已知⊙O₁、⊙O₂的半径分别为5cm、8cm，且它们的圆心距为8cm，则⊙O₁与⊙O₂的位置关系为()

A．外离　　 B．相交　　 C．相切　　　　 D．内含

4．下列事件中，必须事件是()

A．打开电视，它正在播广告　　 B．掷两枚质地均匀的正方体骰子，点数之和一定大于6

C．早晨的太阳从东方升起　　　　 D．没有水分，种子发芽

3．如图，由几个相同的小立方块所搭成的物体的俯视图是()

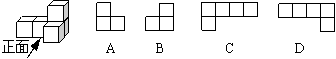
2．下列计算正确的是

A．x⁴+x²＝x⁶　　 B．x⁴－x²＝x²　　 C．x⁴·x²＝x⁸　　　　 D．(x⁴) ²＝x⁸

1．(10·苏·扬州)－5的倒数是

A．－5　　　 B．5　　　　 C．－ 　　　　　 D．

28．(本题10分)如图，已知二次函数y=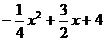的图象与y轴交于点A，与x轴

　 交于B、C两点，其对称轴与x轴交于点D，连接AC．

　 (1)点A的坐标为_______ ，点C的坐标为_______ ；

　 (2)线段AC上是否存在点E，使得△EDC为等腰三角形?若存在，求出所有符合条件的点E的坐标；若不存在，请说明理由；

　 (3)点P为x轴上方的抛物线上的一个动点，连接PA、PC，若所得△PAC的面积为S，则S取何值时，相应的点P有且只有2个?

27．(本题8分)如图①，将边长为4cm的正方形纸片ABCD沿EF折叠(点E、F分别在边AB、CD上)，使点B落在AD边上的点 M处，点C落在点N处，MN与CD交于点P， 连接EP．

　 (1)如图②，若M为AD边的中点，

　　 ①,△AEM的周长=_____cm；

　　 ②求证：EP=AE+DP；

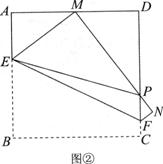　 (2)随着落点M在AD边上取遍所有的位置(点M不与A、D重合)，△PDM的周长是否发生变化?请说明理由．

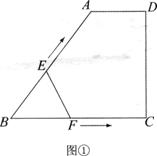
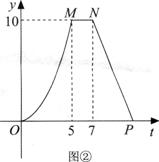
26．(本题8分)如图①，梯形ABCD中，∠C=90°．动点E、F同时从点B出发，点E沿折线　 BA-AD-DC运动到点C时停止运动，点F沿BC运动到点C时停止运动，它们运动时的速度都是1 cm/s．设E、F出发t s时，△EBF的面积为y cm²．已知y与t的函数图象如图②所示，其中曲线OM为抛物线的一部分，MN、NP为线段．请根据图中的信息，解答下列问题：

　 (1)梯形上底的长AD=_____cm，梯形ABCD的面积_____cm²；

　 (2)当点E在BA、DC上运动时，分别求出y与t的函数关系式(注明自变量的取值范围)；

　 (3)当t为何值时，△EBF与梯形ABCD的面积之比为1：2.