
7.已知抛物线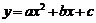 (
(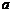 <0)过A(
<0)过A(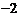 ,0)、O(0,0)、
,0)、O(0,0)、
B(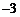 ,
,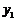 )、C(3,
)、C(3,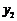 )四点,则
)四点,则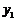 与
与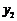 的大小关系是
的大小关系是
A.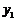 >
>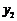 B.
B.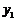
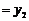 C.
C.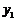 <
<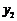 D.不能确定
D.不能确定
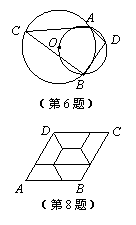
6.如图,两圆相交于A,B两点,小圆经过大圆的圆心O,点C,D分
别在两圆上,若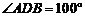 ,则
,则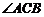 的度数为
的度数为
A.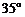 B.
B.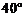 C.
C.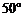 D.
D.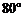
5. 平面直角坐标系中,点A的坐标为(4,3),将线段OA绕原点O顺时针旋转
平面直角坐标系中,点A的坐标为(4,3),将线段OA绕原点O顺时针旋转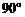 得到
得到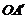 ,则点
,则点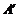 的坐标是
的坐标是
A.(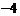 ,3) B.(
,3) B.(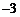 ,4) C.(3,
,4) C.(3,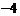 ) D.(4,
) D.(4,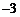 )
)
4.分式方程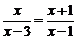 的解为
的解为
A. B.
B.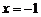 C.
C.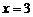 D.
D.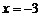
3.一家鞋店对上周某一品牌女鞋的销售量统计如下:
|
尺码/厘米 |
22 |
22.5 |
23 |
23.5 |
24 |
24.5 |
25 |
|
销售量/双 |
1 |
2 |
5 |
11 |
7 |
3 |
1 |
该鞋店决定本周进该品牌女鞋时多进一些尺码为23.5厘米的鞋,影响鞋店决策的统计量是
A.平均数 B.众数 C.中位数 D.方差
2.下列运算正确的是
A. B.
B.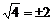 C.
C.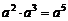 D.
D.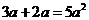
1.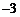 的绝对值是
的绝对值是
A.3 B.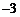 C.
C.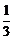 D.
D.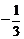
25.(2010.十堰)(本小题满分10分)已知关于x的方程mx2-(3m-1)x+2m-2=0
(1)求证:无论m取任何实数时,方程恒有实数根.
(2)若关于x的二次函数y= mx2-(3m-1)x+2m-2的图象与x轴两交点间的距离为2时,求抛物线的解析式.
(3)在直角坐标系xoy中,画出(2)中的函数图象,结合图象回答问题:当直线y=x+b与(2)中的函数图象只有两个交点时,求b的取值范围.
[答案]解:(1)分两种情况讨论:
①当m=0 时,方程为x-2=0,∴x=2 方程有实数根
②当m≠0时,则一元二次方程的根的判别式
△=[-(3m-1)]2-4m(2m-2)=m2+2m+1=(m+1)2≥0
不论m为何实数,△≥0成立,∴方程恒有实数根
综合①②,可知m取任何实数,方程mx2-(3m-1)x+2m-2=0恒有实数根.
(2)设x1,x2为抛物线y= mx2-(3m-1)x+2m-2与x轴交点的横坐标.
则有x1+x2=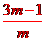 ,x1·x2=
,x1·x2=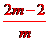
由| x1-x2|=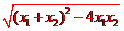 =
=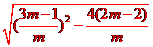 =
=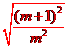 =
=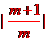 ,
,
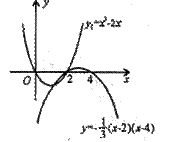 由| x1-x2|=2得
由| x1-x2|=2得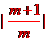 =2,∴
=2,∴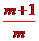 =2或
=2或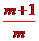 =-2
=-2
∴m=1或m=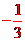
∴所求抛物线的解析式为:y1=x2-2x或y2=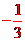 x2+2x-
x2+2x-
即y1= x(x-2)或y2=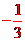 (x-2)(x-4)其图象如右图所示.
(x-2)(x-4)其图象如右图所示.
(3)在(2)的条件下,直线y=x+b与抛物线y1,y2组成的图象只有两个交点,结合图象,求b的取值范围.
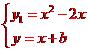 ,当y1=y时,得x2-3x-b=0,△=9+4b=0,解得b=-;
,当y1=y时,得x2-3x-b=0,△=9+4b=0,解得b=-;
同理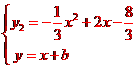 ,可得△=9-4(8+3b)=0,得b=-.
,可得△=9-4(8+3b)=0,得b=-.
观察函数图象可知当b<-或b>-时,直线y=x+b与(2)中的图象只有两个交点.
由
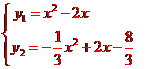
当y1=y2时,有x=2或x=1
当x=1时,y=-1
所以过两抛物线交点(1,-1),(2,0)的直线y=x-2,
综上所述可知:当b<-或b>-或b=-2时,直线y=x+b与(2)中的图象只有两个交点.
24.(2010.十堰)(本小题满分9分)如图,已知⊙O1与⊙O2都过点A,AO1是⊙O2的切线,⊙O1交O1O2于点B,连结AB并延长交⊙O2于点C,连结O2C.
(1)求证:O2C⊥O1O2;
(2)证明:AB·BC=2O2B·BO1;
(3)如果AB·BC=12,O2C=4,求AO1的长.
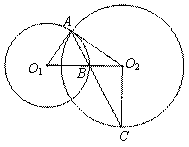

解:(1)∵AO1是⊙O2的切线,∴O1A⊥AO2 ∴∠O2AB+∠BAO1=90°
又O2A=O2C,O1A=O1B,∴∠O2CB=∠O2AB,∠O2BC=∠ABO1=∠BAO1
∴∠O2CB+∠O2BC=∠O2AB+∠BAO1=90°,∴O2C⊥O2B,即O2C⊥O1O2
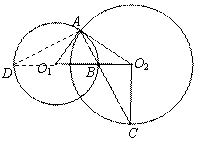 (2)延长O2O1交⊙O1于点D,连结AD.
(2)延长O2O1交⊙O1于点D,连结AD.
∵BD是⊙O1直径,∴∠BAD=90°
又由(1)可知∠BO2C=90°
∴∠BAD=∠BO2C,又∠ABD=∠O2BC
∴△O2BC∽△ABD
∴
∴AB·BC=O2B·BD 又BD=2BO1
∴AB·BC=2O2B·BO1
(3)由(2)证可知∠D=∠C=∠O2AB,即∠D=∠O2AB,又∠AO2B=∠DO2A
∴△AO2B∽△DO2A
∴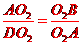
∴AO22=O2B·O2D
∵O2C=O2A
∴O2C2=O2B·O2D ①
又由(2)AB·BC=O2B·BD ②
由①-②得,O2C2-AB·BC= O2B2 即42-12=O1B2
∴O2B=2,又O2B·BD=AB·BC=12
∴BD=6,∴2AO1=BD=6 ∴AO1=3
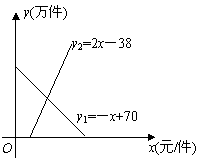
23.(2010.十堰)(本小题满分8分)如图所示,某地区对某种药品的需求量y1(万件),供应量y2(万件)与价格x(元/件)分别近似满足下列函数关系式:y1=-x + 70,y2=2x-38,需求量为0时,即停止供应.当y1=y2时,该药品的价格称为稳定价格,需求量称为稳定需求量.
(1)求该药品的稳定价格与稳定需求量.
(2)价格在什么范围内,该药品的需求量低于供应量?
(3)由于该地区突发疫情,政府部门决定对药品供应方提供价格补贴来提高供货价格,以利提高供应量.根据调查统计,需将稳定需求量增加6万件,政府应对每件药品提供多少元补贴,才能使供应量等于需求量.

解:(1)由题可得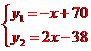 ,
,
当y1=y2时,即-x+70=2x-38
∴3x=108,∴x=36
当x=36时,y1=y2=34,所以该药品的稳定价格为36元/件,稳定需求量为34万件.
(2)令y1=0,得x=70,由图象可知,当药品每件价格在大于36元小于70元时,该药品的需求量低于供应量.
(3)设政府对该药品每件价格补贴a元,则有
 ,解得
,解得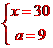
所以政府部门对该药品每件应补贴9元.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com