
27.(14分)如图,已知抛物线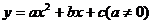 的顶点坐
的顶点坐
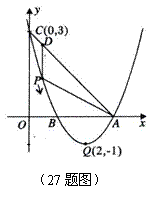 标为Q
标为Q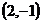 ,且与
,且与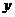 轴交于点C
轴交于点C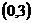 ,与
,与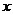 轴交于A、B两
轴交于A、B两
点(点A在点B的右侧),点P是该抛物线上一动点,从点C
沿抛物线向点A运动(点P与A不重合),过点P作PD∥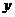 轴,
轴,
交AC于点D.
(1)求该抛物线的函数关系式;
(2)当△ADP是直角三角形时,求点P的坐标;
(3)在问题(2)的结论下,若点E在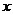 轴上,点F在抛物线上,
轴上,点F在抛物线上,
问是否存在以A、P、E、F为顶点的平行四边形?若存在,
求点F的坐标;若不存在,请说明理由.
机密★启用前
遵义市2010初中毕业生学业(升学)统一考试
26.(12分)如图,在△ABC中,∠C=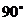 ,AC+BC=8,点O是
,AC+BC=8,点O是
斜边AB上一点,以O为圆心的⊙O分别与AC、BC相切于
点D、E.
(1)当AC=2时,求⊙O的半径;
(2)设AC=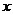 ,⊙O的半径为
,⊙O的半径为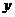 ,求
,求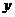 与
与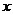 的函数关系式.
的函数关系式.
25.(10分)某酒厂每天生产A、B两种品牌的白酒共600瓶,A、B两种品牌的白酒每瓶的成本和利润如下表:
|
|
A |
B |
|
成本(元/瓶) |
50 |
35 |
|
利润(元/瓶) |
20 |
15 |
设每天生产A种品牌的白酒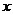 瓶,每天获利
瓶,每天获利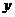 元.
元.
(1)请写出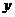 关于
关于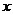 的函数关系式;
的函数关系式;
(2)如果该酒厂每天至少投入成本26400元,那么每天至少获利多少元?
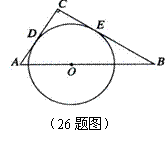
24.(10分)如图(1),在△ABC和△EDC中,AC=CE=CB=CD,∠ACB=∠ECD=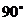 ,AB与CE交于F,ED与AB、BC分别交于M、H.
,AB与CE交于F,ED与AB、BC分别交于M、H.
(1)求证:CF=CH;
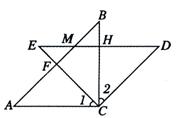
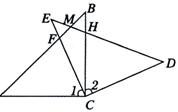 (2)如图(2),△ABC不动,将△EDC绕点C旋转到∠BCE=
(2)如图(2),△ABC不动,将△EDC绕点C旋转到∠BCE= 时,试判断四边形ACDM是什么四边形?并证明你的结论.
时,试判断四边形ACDM是什么四边形?并证明你的结论.
|
|
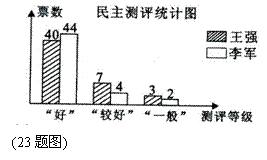
23.(10分)某校七年级(1)班为了在王强和李军两同学中选班长,进行了一次“演讲”与“民主测评”活动,A、B、C、D、E五位老师作为评委对王强、李军的“演讲”打分;该班50名同学分别对王强和李军按“好”、“较好”、“一般”三个等级进行民主测评。统计结果如下图、表.计分规则:
①“演讲”得分按“去掉一个最高分和一个最低分后计算平均分”;
②“民主测评”分=“好”票数×2分+“较好”票数×1分+“一般”票数×0分;
③综合分=“演讲”得分×40%+“民主测评”得分×60%.
解答下列问题:
(1)演讲得分,王强得 ▲ 分;李军得 ▲ 分;
(2)民主测评得分,王强得 ▲ 分; 李军得 ▲ 分;
(3)以综合得分高的当选班长,王强和李军谁能当班长?为什么?
 演讲得分表(单位:分)
演讲得分表(单位:分)
|
评委 姓名 |
A |
B |
C |
D |
E |
|
王强 |
90 |
92 |
94 |
97 |
82 |
|
李军 |
89 |
82 |
87 |
96 |
91 |
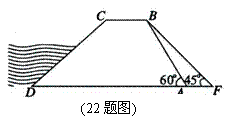
22.(10分)如图,水坝的横断面是梯形,背水坡AB的坡
角∠BAD=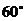 ,坡长AB=
,坡长AB=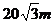 ,为加强水坝强度,
,为加强水坝强度,
将坝底从A处向后水平延伸到F处,使新的背水坡
的坡角∠F= ,求AF的长度(结果精确到1米,
,求AF的长度(结果精确到1米,
参考数据: 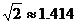 ,
,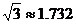 ).
).
21.(8分)在一个不透明的盒子里,装有三个分别写有数字-1、0、1的乒乓球(形状、大小一样),先从盒子里随机取出一个乒乓球,记下数字后放回盒子,摇匀后再随机取 出一个乒乓球,记下数字.
(1)请用树状图或列表的方法求两次取出乒乓球上的数字相同的概率;
(2)求两次取出乒乓球上的数字之积等于0的概率.
20.(8分)解方程: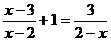
19.(6分)计算: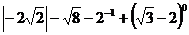
18.如图,在第一象限内,点P,M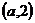 是双曲线
是双曲线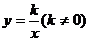 上的两点,PA⊥
上的两点,PA⊥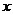 轴于点A,MB⊥
轴于点A,MB⊥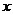 轴于点B,PA与OM交于点C,则△OAC的面积为 ▲ .
轴于点B,PA与OM交于点C,则△OAC的面积为 ▲ .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com