
2.下列运算中,正确的是( )中考资源网.
(A)中考资源网x3·x2=x5 (B)中考资源网x+x2=x3 (C)中考资源网2x3÷x2=x (D)中考资源网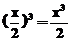
1.某年哈尔滨市一月份的平均气温为-18℃,三月份的平均气温为2℃,则三月份的平均气温比
一月份的平均气温高()中考资源网.
(A)中考资源网16℃ (B)中考资源网20℃ (C)中考资源网一16℃ (D)中考资源网一20℃
26.(本题满分12分,任选一题作答)
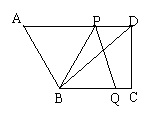
①如图,矩形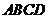 中,
中,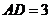 厘米,
厘米,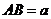 厘米(
厘米(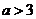 ).动点
).动点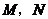 同时从
同时从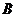 点出发,分别沿
点出发,分别沿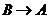 ,
,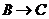 运动,速度是
运动,速度是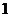 厘米/秒.过
厘米/秒.过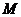 作直线垂直于
作直线垂直于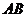 ,分别交
,分别交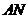 ,
,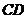 于
于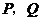 .当点
.当点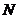 到达终点
到达终点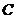 时,点
时,点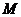 也随之停止运动.设运动时间为
也随之停止运动.设运动时间为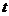 秒.
秒.
(1)若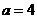 厘米,
厘米,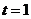 秒,则
秒,则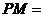 ______厘米;
______厘米;
(2)若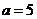 厘米,求时间
厘米,求时间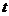 ,使
,使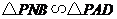 ,并求出它们的相似比;
,并求出它们的相似比;
(3)若在运动过程中,存在某时刻使梯形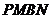 与梯形
与梯形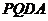 的面积相等,求
的面积相等,求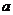 的取值范围;
的取值范围;
(4)是否存在这样的矩形:在运动过程中,存在某时刻使梯形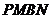 ,梯形
,梯形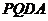 ,梯形
,梯形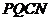 的面积都相等?若存在,求
的面积都相等?若存在,求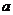 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
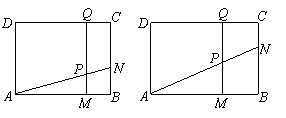
②如图,在等腰梯形ABCD中,AB=DC=5,AD=4,BC=10. 点E在下底边BC上,点F在腰AB上.
(1)若EF平分等腰梯形ABCD的周长,设BE长为x,试用含x的代数式表示△BEF的面积;
(2)是否存在线段EF将等腰梯形ABCD的周长和面积同时平分?若存在,求出此时BE的长;若不存在,请说明理由;
(3)是否存在线段EF将等腰梯形ABCD的周长和面积同时分成1∶2的两部分?若存在,求出此时BE的长;若不存在,请说明理由.
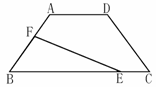
③如图,在直角梯形ABCD中,AD∥BC,∠C=90°,BC=16,DC=12,AD=21。动点P从点D出发,沿射线DA的方向以每秒2两个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,点P,Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动。设运动的时间为t(秒).
 (1)设△BPQ的面积为S,求S与t之间的函数关系式
(1)设△BPQ的面积为S,求S与t之间的函数关系式
(2)当t为何值时,以B,P,Q三点为顶点的三角形是等腰三角形?
(3)当线段PQ与线段AB相交于点O,且2AO=OB时,求t的值.
(4)是否存在时刻t,使得PQ⊥BD?若存在,求出t的值;若不存在,请说明理由.
25.(本题10分)已知一次函数y1=ax+b的图象与反比例函数y2=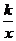 的图象相交于A、B两点,坐标分别为
的图象相交于A、B两点,坐标分别为
(-2,4)、(4,-2)。
(1)求两个函数的解析式;
(2)结合图象写出y1<y2时,x的取值范围;
 (3)求△AOB的面积;
(3)求△AOB的面积;
(4)是否存在一点P,使以点A﹑B﹑O﹑P为顶点的四边形为菱形?
若存在,求出顶点P的坐标;若不存在,请说明理由。
24.(本题8分)小华将勤工俭学挣得的100元钱按一年定期存入银行,到期后取出50元来购买学习用品,剩下的50元和应得的利息又全部按一年定期存入银行,若存款的年利率又下调到原来的一半,这样到期后可得本息和63元,求第一次存款的年利率(不计利息税)
23. (本题7分)
(本题7分)
①如图,四形ABCD中,对角线相交于点O,E、F、G、H分别是AD,BD, BC,AC的中点。
(1)求证:四边形EFGH是平行四边形;
(2)当四边形ABCD满足一个什么条件时,四边形EFGH是菱形? 并证明你的结论。 (23题图)
②如图,在Rt△ABC中,∠ACB=900,AC=BC,D为BC中点,CE⊥AD于E,BF∥AC,
交AC的延长线与点F。求证:AB垂直平分DF.
22.(本题7分)端午节吃粽子是中华民族的传统习俗,五月初五早上,奶奶为小明准备了四只粽子:一只肉馅,一只香肠馅,两只红枣馅,四只粽子除内部馅料不同外其他均一切相同.小明喜欢吃红枣馅的粽子.
(1)请你用树状图或列表法为小明预测一下吃两只粽子刚好都是红枣馅的概率;
(2)在吃粽子之前,小明准备用一格均匀的正四面体骰子(如图所示)进行吃粽子的模拟试验,规定:掷得点数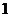 向上代表肉馅,点数
向上代表肉馅,点数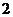 向上代表香肠馅,点数
向上代表香肠馅,点数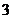 ,
,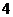 向上代表红枣馅,连续抛掷这个骰子两次表示随机吃两只粽子,从而估计吃两只粽子刚好都是红枣馅的概率.你认为这样模拟正确吗?试说明理由.
向上代表红枣馅,连续抛掷这个骰子两次表示随机吃两只粽子,从而估计吃两只粽子刚好都是红枣馅的概率.你认为这样模拟正确吗?试说明理由.
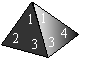
(22题图)
21.(本题6分)旗杆、树和竹杆都垂直于地面且一字排列,在路灯下树和竹杆的影子的方位和长短如图所示. 请根据图上的信息标出灯泡的位置(点P表示),再作出旗杆的影子(字母表示).(不写作法,保留作图痕迹)
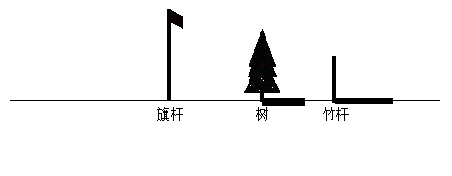
(21题图)
20. (本题6分) 用反证法证明:等腰三角形的底角是锐角。
19.解方程:(每小题4分,共8分)
(1)(2x+3)2-25=0 (2)3x2-5x+5=7
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com