13．(2009年重庆模拟)如图46所示，(a)图表示某物体在x轴方向上分速度的v－t图象，(b)图表示该物体在y轴上分速度的v－t图象．求：

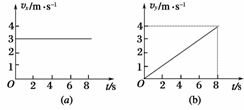
图46

(1)物体在t＝0时的速度．

(2)t＝8 s时物体的速度．

(3)前4 s内物体的位移．

解析：根据图象可以知道，物体在x方向上以3 m/s的速度做匀速直线运动，在y方向上做初速度为0、加速度为0.5 m/s²的匀加速直线运动，合运动是曲线运动．

(1)在t＝0时刻，物体的速度大小v＝＝

3 m/s，方向与x轴同向．

(2)在t＝8 s时刻，物体在x方向的速度为3 m/s，物体在y方向的速度为4 m/s，所以物体的速度大小为v＝＝5 m/s，方向：tanθ＝＝，θ＝arctan，θ为v与x轴夹角．

(3)在4 s的时间内物体在x方向发生的位移为x＝12 m，物体在y方向发生的位移为y＝at²＝4 m，所以4 s内物体发生的位移大小为s＝＝4 m，方向：tanβ＝＝，β＝arctan，β为位移与x方向夹角．

答案：(1)大小为3 m/s，方向与x轴同向

(2)大小为5 m/s，方向与x轴夹角为arctan

(3)大小为4 m/s，方向与x轴夹角为arctan

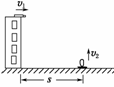
图47

12．一阶梯如图45所示，其中每级台阶的高度和宽度都是0.4 cm，一小球以水平速度v飞出，欲打在第四台阶上，则v的取值范围是(　)

A. m/s<v<2 m/s

B．2 m/s<v≤3.5 m/s

C. m/s<v< m/s

D．2 m/s<v< m/s

解析：由题意知为使小球打在第四级台阶上，小球水平飞出的距离范围为大于1.2 m小于等于1.6 m，即1.2 m<x≤1.6 m．下落高度为y＝1.6 m，利用x、y的最小值，根据平抛运动规律，求出最小速度v_min＝＝ m/s＝ m/s，最大速度v_max＝＝ m/s＝2 m/s.由此可求得小球打在第四级台阶上速度v的取值范围为 m/s<v<2 m/s.

答案：A

11．如图44所示，A、B为两个挨得很近的小球，并列放于光滑斜面上，斜面足够长，在释放B球的同时，将A球以某一速度v₀水平抛出，当A球落于斜面上的P点时，B球的位置位于(　)

A．P点以下　　　　　　　　　　　 B．P点以上

C．P点　 　　　　　　　　　　　　　　　　　　　　 D．由于v₀未知，故无法确定

解析：设A点落在P点的时间为t_A，AP的竖直位移为y；B球滑到P点的时间为t_B，BP的竖直位移也为y，则：t_A＝，t_B＝＝>t_A(θ为斜面倾角)．

答案：B

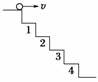
图45

10．(2009年海淀区模拟)民族运动会上有一个骑射项目，运动员骑在奔驰的马背上，弯弓放箭射击侧向的固定目标．假设运动员骑马奔驰的速度为v₁，运动员静止时射出的弓箭速度为v₂.直跑道离固定目标的最近距离为d.要想在最短的时间内射中目标，则运动员放箭处离目标的距离应该为(　)

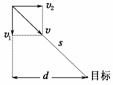
图43

A.　　　　　　　　　　　　　　　　　　 B.

C.　 　　　　　　　　　　　　　　　　　　　　　　 D.

解析：要想在最短时间内射中目标，运动员放箭时应使箭的合速度方向对准目标，如图43则有s＝vt＝·.

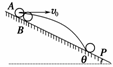
图44

答案：B

9．执行救灾任务的飞机，逆风做水平匀速直线飞行，相隔0.5 s先后释放形状和质量完全相同的两箱救灾物资1号箱和2号箱．假设风力保持不变，这两箱物资在空中下落时，地上的人沿着飞机飞行的方向看(　)

A．1号箱在2号箱的正下方

B．两箱间的水平距离保持不变

C．两箱间的水平距离越来越大

D．两箱间的水平距离越来越小

解析：完全释放救灾物资后经历时间t，两箱水平距离Δs＝[v₀t－at²]－[v₀(0.5+t)－a(t+0.5)²]＝a(t+0.5)²－at²－0.5v₀＝at+a－0.5v₀，所以随着时间t的增大，Δs增大．

答案：C

8．如图42所示，从一根内壁光滑的空心竖直钢管A的上端边缘，沿直径方向向管内水平抛入一钢球．球与管壁多次相碰后落地(球与管壁相碰时间不计)，若换一根等高但较粗的内壁光滑的钢管B，用同样的方法抛入此钢球，则运动时间(　)

A．在A管中的球运动时间长

B．在B管中的球运动时间长

C．在两管中的球运动时间一样长

D．无法确定

解析：小球做平抛运动，平抛运动可分解为水平方向的匀速运动和竖直方向的自由落体运动．球跟管壁碰撞中受水平方向弹力作用，只改变水平方向速度大小，而竖直方向始终仅受重力作用，保持自由落体运动．由公式h＝gt²，得t＝，因A、B等高，故t相同，应选C.

答案：C

7．(2009年贵阳模拟)如图41所示，两小球a、b从直角三角

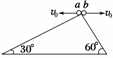
图41

形斜面的顶端以相同大小的水平速率v₀向左、向右水平抛出，分别落在两个斜面上，三角形的两底角分别为30°和60°，则两小球a、b运动时间之比为(　)

A．1∶　 　　　　　　　　　　　　　　　　　　　 B．1∶3

C.∶1　 　　　　　　　　　　　　　　　　　　　　 D．3∶1

解析：设a、b两球运动的时间分别为t_a和t_b，则tan30°＝＝，tan60°＝＝，两式相除得：＝＝.

答案：B

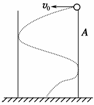
图42

6．如图39所示，一条小船位于200 m宽的河正中A点处，从这里向下游100 m处有一危险区，当时水流速度为4 m/s，为了使小船避开危险区沿直线到达对岸，小船在静水中的速度至少是(　)

A. m/s　 　　　　　　　　　　　　　　　　　　 B. m/s

C．2 m/s　 　　　　　　　　　　　　　　　　　　　　 D．4 m/s

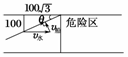
图40

解析：如图40所示，tanθ＝＝，θ＝30°，故v_船＝v_水sinθ＝4× m/s＝2 m/s.

答案：C

5．质量为m的物体，在F₁、F₂、F₃三个共点力的作用下做匀速直线运动，保持F₁、F₂不变，仅将F₃的方向改变90°(大小不变)后，物体可能做(　)

A．加速度大小为的匀变速直线运动

B．加速度大小为的匀变速直线运动

C．加速度大小为的匀变速曲线运动

D．匀速直线运动

解析：由牛顿第二定律得：a＝＝.显然a恒定，应为匀变速运动．若a的方向与v的方向在一条直线上，则是匀变速直线运动，否则是匀变速曲线运动．

答案：BC

图39

4．图38为一空间探测器的示意图，P₁、P₂、P₃、P₄是四个喷气式发动机，P₁、P₃的连线与空间一固定坐标系的x轴平行，P₂、P₄的连线与y轴平行．每台发动机开动时，都能向探测器提供推力，但不会使探测器转动．开始时，探测器以恒定的速率v₀向正x方向平动．要使探测器改为向正x偏负y60°的方向以原来的速率v₀平动，则可(　)

A．先开动P₁适当时间，再开动P₄适当时间

B．先开动P₃适当时间，再开动P₂适当时间

C．开动P₄适当时间

D．先开动P₃适当时间，再开动P₄适当时间

解析：P₁、P₂、P₃、P₄都是喷气式发动机，是利用反冲作用使探测器获得速度的，从题图中看出：P₁开动时探测器获得负x方向的速度；P₄开动时探测器获得负y方向的速度，要使探测器沿正x偏负y60°方向以原来的速率v₀平动，这时的速度应是探测器在正x方向的速度v_x与负y方向的速度v_y的合成，且合速度值应为v₀.因此必须使正x方向速度减小到适当值，使负y方向速度增加到适当值，也就是要开动P₁适当时间，再开动P₄适当时间，选A.

答案：A