
7.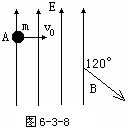 如图6-3-8所示,质量为m,电量为e的电子,从A点以速度v0垂直场强方向射入匀强电场中,从B点射出电场时的速度方向与电场线成1200角,则A、B两点间的电势差是多少?
如图6-3-8所示,质量为m,电量为e的电子,从A点以速度v0垂直场强方向射入匀强电场中,从B点射出电场时的速度方向与电场线成1200角,则A、B两点间的电势差是多少?
解析:电子从A运动到B的过程中,电场力对电子做正功,由动能定理和几何关系有:
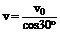 ;
; 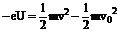 ;
; 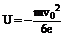
6.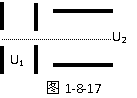 如图1-8-17所示,电子在电势差为U1的加速电场中由静止开始运动,然后射入电势差为U2的两块平行极板间的偏转匀强电场中,在满足电子能射出平行极板区的条件下,下述四种情况中,一定能使电子的偏转角θ变大的是( B )
如图1-8-17所示,电子在电势差为U1的加速电场中由静止开始运动,然后射入电势差为U2的两块平行极板间的偏转匀强电场中,在满足电子能射出平行极板区的条件下,下述四种情况中,一定能使电子的偏转角θ变大的是( B )
A.U1变大、U2变大 B.U1变小、U2变大
C.U1变大、U2变小 D.U1变小、U2变小
5.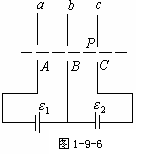 如图1-9-6所示,三个平行金属板a、b、c,ab相距d1,bc相距d2,d1 = d2三个金属板上分别有三个小孔A、B、C三个金属板接到电动势为
如图1-9-6所示,三个平行金属板a、b、c,ab相距d1,bc相距d2,d1 = d2三个金属板上分别有三个小孔A、B、C三个金属板接到电动势为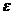 1和
1和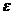 2的两个电源上,
2的两个电源上,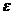 1 <
1 < 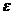 2,在A孔右侧放一个带负电质点,由静止释放后,质点将向右运动,穿过B孔,到达P后再返回A孔,则有( BD)
2,在A孔右侧放一个带负电质点,由静止释放后,质点将向右运动,穿过B孔,到达P后再返回A孔,则有( BD)
A.将b板平行向右移动一小段距离,再释放带电质点,质点仍将运动到P点返回
B.将b板平行向右移动一小段距离,再释放带电质点,质点将向右运动,并越过P点返回
C.若将b板平行向右移动足够远,再释放带电质点,质点能够穿过C孔
D.若将带电质点放在C孔左侧,由静止释放,它一定能穿过A孔
4. 如图1-9-5所示,有三个质量相等,分别带正电,负电和不带电的小球,从上、下带电平行金属板间的P点.以相同速率垂直电场方向射入电场,它们分别落到A、B、C三点,则(AC)
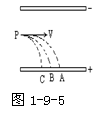 A.A带正电、B不带电、C带负电
A.A带正电、B不带电、C带负电
B.三小球在电场中运动时间相等
C.在电场中加速度的关系是 aA>aB>aC
D.到达正极板时动能关系EkA>EkB>EkC
综合跃升
3. (2007海南 6)一平行板电容器中存在匀强电场,电场沿竖直方向。两个比荷(即粒子的电荷量与质量之比)不同的带正电的粒子a和b,从电容器边缘的P点(如图)以相同的水平速度射入两平行板之间。测得a和b与电容器的撞击点到入射点之间的水平距离之比为1∶2。若不计重力,则a和b的比荷之比是( D
)
(2007海南 6)一平行板电容器中存在匀强电场,电场沿竖直方向。两个比荷(即粒子的电荷量与质量之比)不同的带正电的粒子a和b,从电容器边缘的P点(如图)以相同的水平速度射入两平行板之间。测得a和b与电容器的撞击点到入射点之间的水平距离之比为1∶2。若不计重力,则a和b的比荷之比是( D
)
A.1∶2 B.1∶1 C.2∶1 D.4∶1
2.对公式 的适用条件,正确的有
(
D )
的适用条件,正确的有
(
D )
A.只适用于匀强电场中,v0=0的带电粒子被加速
B.只适用于匀强电场中,粒子运动方向和场强方向平行的情况
C.只适用于匀强电场中,粒子运动方向和场强方向垂直的情况
D.适用于任何电场中,v0=0的带电粒子被加速
案例精析:
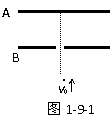 [例1] 如图1-9-1所示,水平放置的A、B两平行板相距h,上板A带正电,现有质量为m、带电量为+q的小球在B板下方距离B板为H处,以初速υ0竖直向上从B板小孔进入板间电场,欲使小球刚好打到A板,A、B间电势差为多少?
[例1] 如图1-9-1所示,水平放置的A、B两平行板相距h,上板A带正电,现有质量为m、带电量为+q的小球在B板下方距离B板为H处,以初速υ0竖直向上从B板小孔进入板间电场,欲使小球刚好打到A板,A、B间电势差为多少?
解析 对小球运动的全过程根据动能定理列式
-mg(H+h)-qUAB=0-mυ02/2
UAB=m[υ02-2g(H+h)]/(2q)
拓展 试用牛顿运动定律和运动学公式重解一下。
 [例2]一束电子流在经U1=5000V的加速电压加速后,在距两极板等距处垂直进入平行板间的匀强电场,如图1-9-3所示,若两板间d=1.0cm ,板长l=5.0cm,那么,要使电子能从平行板间的边缘飞出,两个极板上最多能加多大电压?
[例2]一束电子流在经U1=5000V的加速电压加速后,在距两极板等距处垂直进入平行板间的匀强电场,如图1-9-3所示,若两板间d=1.0cm ,板长l=5.0cm,那么,要使电子能从平行板间的边缘飞出,两个极板上最多能加多大电压?
[解析]解析:电子经U1加速时,根据动能定理可得:
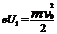
电子飞入平行板在水平方向:l=v0t
在竖直方向: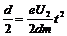
由以上各式解得:U2=400V
即要使电子能飞出,所加电压最大为400V。
[点评]此题是一个较典型的带电粒子先加速再偏转的题目。通过该题认真体会求解这类问题的思路和方法,并注意解体格式的规范化。粒子恰能飞出极板和粒子恰不能飞出极板,对应着同一临界状态,根据题意找出临界状态,由临界状态来确定极值,也是求解极值问题的常用方法。
 [例3]两平行金属板A、B水平放置,一个质量m=5×10-6kg的带电微粒以υ0=2m/s的水平初速度从两板正中央位置射入电场,如图1-9-2所示,A、B两板间的距离d=4cm,板长L=10cm。求:
[例3]两平行金属板A、B水平放置,一个质量m=5×10-6kg的带电微粒以υ0=2m/s的水平初速度从两板正中央位置射入电场,如图1-9-2所示,A、B两板间的距离d=4cm,板长L=10cm。求:
(1)当A、B间的电压UAB=1000V时,微粒恰好不偏转,沿图中直线射出电场,求该粒子的电量。
(2)令B板接地,欲使该微粒射出偏转电场,求B板所加电势的范围。
解析:(1)当UAB=1000V时,重力跟电场力平衡,微粒沿初速方向做匀速直线运动,由qUAB/d=mg得:q=mgd/UAB=2×10-9C。因重力方向竖直向下,故电场力方向必须竖直向上。又场强方向竖直向下(UAB>0),所以微粒带负电。
(2)当qE>mg时,带电微粒向上偏。设微粒恰好从上板右边缘飞出时A板电势为φ1,因φB=0,所以UAB=φ1。此时,微粒在水平方向做匀速运动,在竖直方向作加速度a=qφ1/(md)-g的匀加速运动,由d/2=at2/2 和t=L/υ0得φ1=(mυ02d2+mgdL2)/qL2=2600V。
当qE<mg时,带电微粒向下偏转,竖直方向加速度a=g-qφ2/md,同理可得φ2=600V。
所以,要使微粒射出偏转电场,A板电势φA应满足:600V<φA<2600V。
拓展 请确定射出电场的带电微粒的动能值范围。
三维达标:
基础练习
1.一带电粒子在电场中只受电场力作用时,它可能出现的运动状态是 ( BCD )
A.匀速直线运动 B.匀加速直线运动
C.匀变速曲线运动 D.匀速圆周运动
课堂探究:
15.图48为跳台滑雪雪道一部分,曲线雪道ABC为助滑加速雪道,CD为倾角θ=30°的斜面雪道,CD雪道下面与平滑缓冲雪道衔接.滑雪运动员由助滑雪道ABC上的A点由静止开始自由下滑,不计飞行中的空气阻力,已知运动员由C点水平飞出后经2 s刚好距离CD雪道最远,(g取10 m/s2),试分析:
(1)运动员离开C点时的速度;
(2)运动员由C点水平飞出后经多长时间落到斜面CD上.
解析:(1)设运动员由C点水平飞出的速度为v0,飞出2 s后的竖直速度为vy,当运动员距离雪道CD最远时其实际速度与斜面平行,由平抛运动规律有vy=gt1 ①,=tanθ ②
由①②联立代入数据得v0=20 m/s.
(2)设运动员在斜面CD上的落点与C点的距离为s,由平抛运动规律有ssinθ=gt2③
scosθ=v0t④
由①②③④联立代入数据得t=4 s.
答案:(1)20 m/s (2)4 s
14.(2009年衡阳质检)国家飞碟射击队在进行模拟训练时用如图47所示装置进行.被训练的运动员在高H=20 m的塔顶,在地面上距塔水平距离为s处有一个电子抛靶装置,圆形靶可被以速度v2竖直向上抛出.当靶被抛出的同时,运动员立即用特制手枪沿水平方向射击,子弹速度v1=100 m/s.不计人的反应时间、抛靶装置的高度及子弹在枪膛中的运动时间,且忽略空气阻力及靶的大小(g取10 m/s2).
(1)当s取值在什么范围内,无论v2为何值都不能被击中?
(2)若s=100 m,v2=20 m/s,试通过计算说明靶能否被击中?
解析:(1)若抛靶装置在子弹的射程以外,则不论抛靶速度为何值,都无法击中.
H=gt2,x=v1t
s>x=v1=200 m
即s>200 m,无论v2为何值都不能被击中.
(2)若靶能被击中,则击中处应在抛靶装置的正上方,设经历的时间为t1,则:s=v1t1,t1== s=1 s
y1=gt=×10×12 m=5 m
y2=v2t1-gt=20×12 m-×10×12 m=15 m
因为y1+y2=5 m+15 m=20 m=H,所以靶恰好被击中.
答案:(1)s>200 m (2)恰好击中

图48
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com