
(二)填空是:
5、(06安徽)函数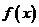 对于任意实数
对于任意实数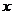 满足条件
满足条件 ,若
,若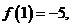 则
则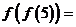 _______________。
_______________。
(一)选择题:
1、(07全国Ⅰ)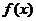 ,
,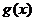 是定义在
是定义在 上的函数,
上的函数,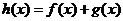 ,则“
,则“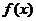 ,
,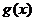 均为偶函数”是“
均为偶函数”是“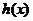 为偶函数”的( )
为偶函数”的( )
A、充要条件 B、充分而不必要的条件
C、必要而不充分的条件 D、既不充分也不必要的条件
2、(06湖北10)关于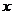 的方程
的方程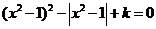 ,给出下列四个命题:( A )
,给出下列四个命题:( A )
①存在实数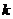 ,使得方程恰有2个不同的实根;
,使得方程恰有2个不同的实根;
②存在实数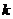 ,使得方程恰有4个不同的实根;
,使得方程恰有4个不同的实根;
③存在实数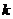 ,使得方程恰有5个不同的实根;
,使得方程恰有5个不同的实根;
④存在实数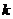 ,使得方程恰有8个不同的实根;
,使得方程恰有8个不同的实根;
其中假命题的个数是
A、0 B、1 C、2 D、3
3、(06辽宁)与方程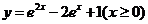 的曲线关于直线
的曲线关于直线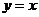 对称的曲线的方程为
对称的曲线的方程为
A、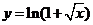 B、
B、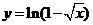 C、
C、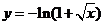 D、
D、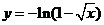
4、(06天津10)已知函数 的图象与函数
的图象与函数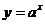 (
(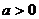 且
且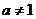 )的图象关于直线
)的图象关于直线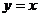 对称,记
对称,记 .若
.若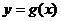 在区间
在区间 上是增函数,则实数
上是增函数,则实数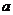 的取值范围是( )
的取值范围是( )
A、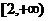 B、
B、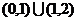 C、
C、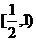 D、
D、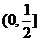
例1、(07山东)给出下列三个等式: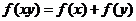 ,
,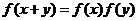 ,
, 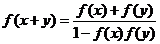 ,下列函数中不满足其中任何一个等式的是( )
,下列函数中不满足其中任何一个等式的是( )
A、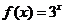 B、
B、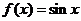 C、
C、 D、
D、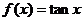
例2、(06全国Ⅰ13)已知函数 ,若
,若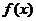 为奇函数,则
为奇函数,则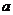 =
;
=
;
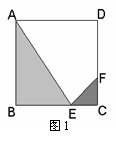 例3、(07上海春)某人定制了一批地砖
例3、(07上海春)某人定制了一批地砖 每块地砖 (如图1所示)是边长为
每块地砖 (如图1所示)是边长为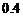 米的正方形
米的正方形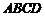 ,点E、F分别在边BC和CD上, △
,点E、F分别在边BC和CD上, △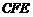 、△
、△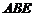 和四边形
和四边形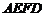 均由单一材料制成,制成△
均由单一材料制成,制成△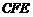 、△
、△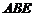 和四边形
和四边形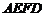 的三种材料的每平方米价格之比依次为3:2:1
的三种材料的每平方米价格之比依次为3:2:1 若将此种地砖按图2所示的形式铺设,能使中间的深色阴影部分成四边形
若将此种地砖按图2所示的形式铺设,能使中间的深色阴影部分成四边形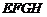

(1) 求证:四边形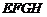 是正方形;
是正方形;
(2) 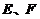 在什么位置时,定制这批地砖所需的材料费用最省?
在什么位置时,定制这批地砖所需的材料费用最省?
 [证明] (1) 图2是由四块图1所示地砖绕点
[证明] (1) 图2是由四块图1所示地砖绕点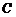 按顺时针旋转
按顺时针旋转 后得到,△
后得到,△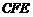 为等腰直角三角形,
为等腰直角三角形,
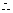 四边形
四边形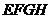 是正方形
是正方形 …… 4分
…… 4分
[解] (2) 设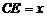 ,则
,则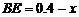 ,每块地砖的费用
,每块地砖的费用
为 ,制成△
,制成△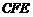 、△
、△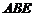 和四边形
和四边形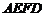 三种材料的每平方米价格依次为3a、2a、a (元),
…… 6分
三种材料的每平方米价格依次为3a、2a、a (元),
…… 6分
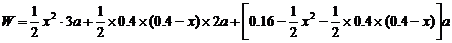
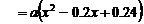 …… 10分
…… 10分
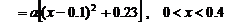

由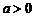 ,当
,当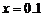 时,
时, 有最小值,即总费用为最省。
有最小值,即总费用为最省。
答:当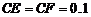 米时,总费用最省
米时,总费用最省 …… 14分
…… 14分
(三)解答题:
6、(06浙江)设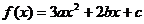 ,若
,若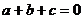 ,
,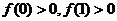 ,求证:
,求证:
(Ⅰ)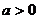 且
且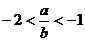 ;
;
(Ⅱ)方程 在(0,1)内有两个实根。
在(0,1)内有两个实根。
(二)填空是:
3、(07四川)若函数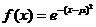 (
(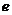 是自然对数的底数)的最大值是m,且f(x)是偶函数,则m+u= ;
是自然对数的底数)的最大值是m,且f(x)是偶函数,则m+u= ;
4、(07江西)设函数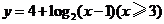 ,则其反函数的定义域为 ;
,则其反函数的定义域为 ;
5、(05江苏17)已知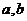 为常数,若
为常数,若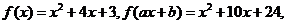 则
则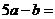
(一)选择题:
1、(06陕西10)已知函数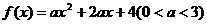 ,若
,若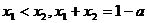 ,则( )
,则( )
A、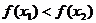 B、
B、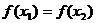 C、
C、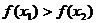 D、
D、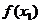 与
与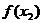 的大小不能确定
的大小不能确定
2、(05全国)设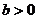 ,二次函数
,二次函数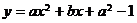 的图像为下列之一
的图像为下列之一
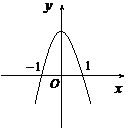
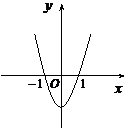
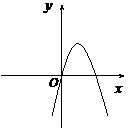
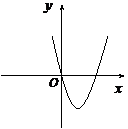
则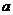 的值为( ) A、
的值为( ) A、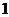 B、
B、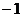 C、
C、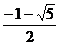 D、
D、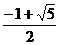
例1、(07广东)设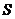 是至少含有两个元素的集合,在
是至少含有两个元素的集合,在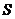 上定义了一个二元运算“*”(即对任意的
上定义了一个二元运算“*”(即对任意的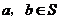 ,对于有序元素对(
,对于有序元素对(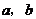 ),在
),在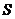 中有唯一确定的元素
中有唯一确定的元素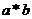 与之对应).若对任意的
与之对应).若对任意的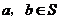 ,有
,有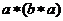
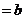 ,则对任意的
,则对任意的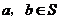 ,下列等式中不恒成立的是( )
A、
,下列等式中不恒成立的是( )
A、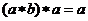 B、
B、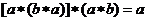
C、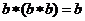 D、
D、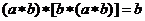
例2、(07广东20)已知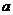 是实数,函数
是实数,函数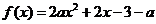 ,如果函数
,如果函数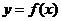 在区间
在区间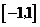 上有零点,求
上有零点,求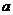 的取值范围.
的取值范围.
解析1:函数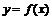 在区间[-1,1]上有零点,即方程
在区间[-1,1]上有零点,即方程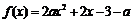 =0在[-1,1]上有解,
=0在[-1,1]上有解,
a=0时,不符合题意,所以a≠0,方程f(x)=0在[-1,1]上有解<=>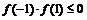 或
或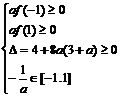
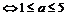 或
或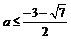 或
或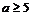
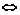
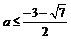 或a≥1.
或a≥1.
所以实数a的取值范围是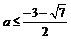 或a≥1.
或a≥1.
解析2:a=0时,不符合题意,所以a≠0,又
∴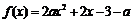 =0在[-1,1]上有解,
=0在[-1,1]上有解,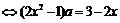 在[-1,1]上有解
在[-1,1]上有解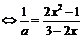 在[-1,1]上有解,问题转化为求函数
在[-1,1]上有解,问题转化为求函数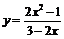 [-1,1]上的值域;设t=3-2x,x∈[-1,1],则
[-1,1]上的值域;设t=3-2x,x∈[-1,1],则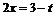 ,t∈[1,5],
,t∈[1,5],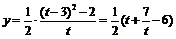 ,
,
设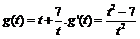 ,
,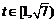 时,
时,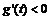 ,此函数g(t)单调递减,
,此函数g(t)单调递减,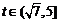 时,
时,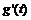 >0,此函数g(t)单调递增,∴y的取值范围是
>0,此函数g(t)单调递增,∴y的取值范围是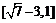 ,∴
,∴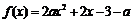 =0在[-1,1]上有解ó
=0在[-1,1]上有解ó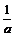 ∈
∈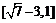
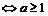 或
或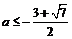 。
。
例3、(07江苏21)已知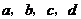 是不全为零的实数,函数
是不全为零的实数,函数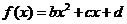 ,
,
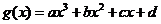 .方程
.方程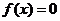 有实数根,且
有实数根,且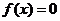 的实数根都是
的实数根都是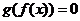 的根;反之,
的根;反之,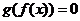 的实数根都是
的实数根都是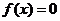 的根。
的根。
(1)求 的值;(3分)
的值;(3分)
(2)若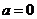 ,求
,求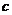 的取值范围;(6分)
的取值范围;(6分)
(3)若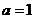 ,
,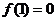 ,求
,求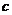 的取值范围。(7分)
的取值范围。(7分)
解:(1)设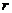 为方程的一个根,即
为方程的一个根,即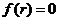 ,则由题设得
,则由题设得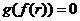 .于是,
.于是,
 ,即
,即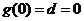 . 所以,
. 所以,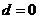 .
.
(2)由题意及(1)知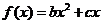 ,
,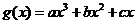 .
.
由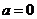 得
得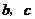 是不全为零的实数,且
是不全为零的实数,且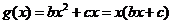 ,
,
则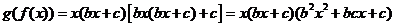 .
.
方程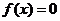 就是
就是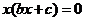 .①
.①
方程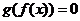 就是
就是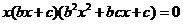 .②
.②
(ⅰ)当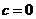 时,
时,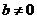 ,方程①、②的根都为
,方程①、②的根都为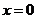 ,符合题意.
,符合题意.
(ⅱ)当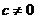 ,
,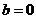 时,方程①、②的根都为
时,方程①、②的根都为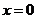 ,符合题意.
,符合题意.
(ⅲ)当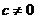 ,
,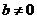 时,方程①的根为
时,方程①的根为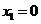 ,
,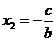 ,它们也都是方程②的根,但它们不是方程
,它们也都是方程②的根,但它们不是方程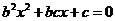 的实数根.
的实数根.
由题意,方程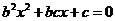 无实数根,此方程根的判别式
无实数根,此方程根的判别式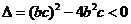 ,得
,得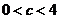 .
.
综上所述,所求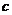 的取值范围为
的取值范围为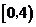 .
.
(3)由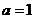 ,
,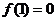 得
得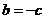 ,
,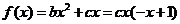 ,
,
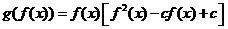 .③
.③
由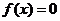 可以推得
可以推得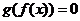 ,知方程
,知方程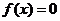 的根一定是方程
的根一定是方程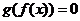 的根.
的根.
当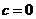 时,符合题意.
时,符合题意.
当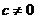 时,
时,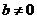 ,方程
,方程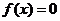 的根不是方程
的根不是方程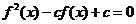 ④
④
的根,因此,根据题意,方程④应无实数根.
那么当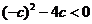 ,即
,即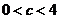 时,
时,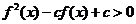 ,符合题意.
,符合题意.
当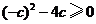 ,即
,即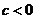 或
或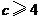 时,由方程④得
时,由方程④得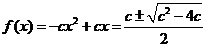 ,
,
即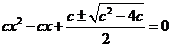 ,⑤
,⑤
则方程⑤应无实数根,所以有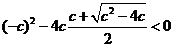 且
且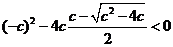 .
.
当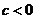 时,只需
时,只需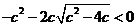 ,解得
,解得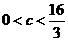 ,矛盾,舍去.
,矛盾,舍去.
当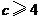 时,只需
时,只需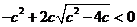 ,解得
,解得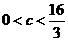 .
.
因此,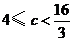 .
.
综上所述,所求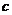 的取值范围为
的取值范围为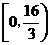 .
.
15.取一根镁条置于坩锅内点燃,得到氧化镁和氮化镁混合物的总质量为
470g. 冷却后加入足量水,将反应产物加热蒸干并灼烧,得到的氧化镁质
量为0.486g。
⑴写出氮化镁与水反应生成氢氧化镁和氨的化学方程式。
⑵计算燃烧所得混合物中氮化镁的质量分数。
14.为测定一种复合氧化物型的磁性粉末材料的组成,称取6.26g样品,将其全部溶于过量稀硝酸后,配成100mL溶液。取50mL溶液,加入过量K2SO4溶液,生成白色沉淀,经过滤、洗涤,烘干后得2.33g固体。另取25mL溶液,加入少许KSCN溶液,显红色。再取余下的25mL溶液,加入过量NaOH溶液,生成红褐色沉淀,将沉淀过滤、洗涤,灼烧后的0.80g固体。请计算并结合推理填写下表。
|
组成该磁性材料的元素是 |
|
|
各元素的质量比是 |
|
|
各元素的原子个数比是 |
|
|
该磁性材料的化学式为 |
|
13.A、B、C、D是四种可溶性离子化合物,其组成中的阴阳离子各不相同,它们在溶液中电离的阴、阳离子分别为Cl-、SO42-、NO32-、OH-、Ag+、Na+、Mg2+、Cu2+。当四种物质的稀溶液反应时产生如下现象①A + B → 产生白色沉淀;②B + D → 产生白色沉淀;③C + D → 产生蓝色沉淀。
由此可以判断(写分子式)A B C D 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com