
6.有两台自动包装机甲与乙,包装重量分别为随机变量ξ1、ξ2,已知Eξ1=Eξ2,Dξ1>Dξ2,则自动包装机________的质量较好.
7.若随机变量A在一次试验中发生的概率为p(0<p<1),用随机变量ξ表示A在1次试验中发生的次数,则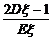 的最大值为
.
的最大值为
.
解:随机变量ξ的所有可能取值为0,1,并且有P(ξ=1)=p,P(ξ=0)=1-p,从而Eξ=0×(1-p)+1×p=p,Dξ=(0-p)2×(1-p)+(1-p)2×p=p-p2.
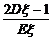 =
=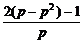 =2-(2p+
=2-(2p+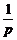 )≤2-2
)≤2-2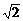
当且仅当2p=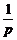 ,即p=
,即p=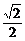 时,
时,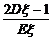 取得最大值2-2
取得最大值2-2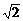 .
.
◆答案:1-3.DBC;
3.一射手对靶射击,直到第一次命中为止每次命中的概率为0.6,现有4颗子弹,命中后的剩余子弹数目ξ的期望为
A.2.44 B.3.376 C.2.376 D.2.4
4. (2006福建)一个均匀小正方体的6个面中,三个面上标以数0,两个面上标以数1,一个面上标以数2.将这个小正方体抛掷2次,则向上的数之积的数学期望是___。
5. (2006四川)设离散型随机变量ξ可能取的值为1,2,3,4.P(ξ=k)=ak+b(k=1,2,3,4),又ξ的数学期望Eξ=3,则a+b=__________
1.(2005江苏)在一次歌手大奖赛上,七位评委为歌手打出的分数如下:9.4,8.4,9.4,9.9,9.6,9.4,9.7,去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为( )
A.9.4, 0.484 B.9.4, 0.016 C.9.5, 0.04 D.9.5, 0.016
2.设导弹发射的事故率为0.01,若发射10次,其出事故的次数为ξ,则下列结论正确的是 ( )
A.Eξ=0.001 B.Dξ=0.099
C.P(ξ=k)=0.01k·0.9910-k D.P(ξ=k)=C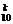 ·0.99k·0.0110-k
·0.99k·0.0110-k
6.二项分布的期望和方差:若ξ-B(n,p),则Eξ=np,
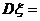 np(1-p)
np(1-p)
7.几何分布的期望和方差:若ξ服从几何分布g(k,p)= 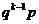 ,则
,则
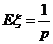 ,
,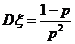
证明: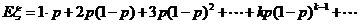
令
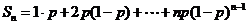
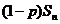
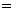
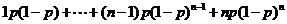
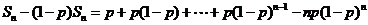

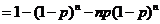
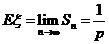 ,
,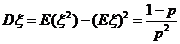
5.会用求和符号Σ:如Eξ=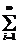 xi pi,Dξ=
xi pi,Dξ=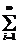 (xi-Eξ)2pi,
(xi-Eξ)2pi,
3.随机变量的数学期望: 一般地,若离散型随机变量ξ的概率分布为
|
ξ |
x1 |
x2 |
… |
xn |
… |
|
P |
p1 |
p2 |
… |
pn |
… |
则称 Eξ=x1p1+x2p2+……+xnpn… 为ξ的数学期望,简称期望.也叫平均数,均值.
(1)数学期望是离散型随机变量的一个特征数,它反映了离散型随机变量取值的平均水平.
(2)期望的一个性质:E(aξ+b)=aEξ+b
(3)求期望的方法步骤: ①确定随机变量的所有取值;
②计算第个取值的概率并列表; ③由期望公式计算期望值。
4. 方差: Dξ=(x1-Eξ)2p1+(x2-Eξ)2p2+…+(xn-Eξ)2pn+…
(1) 标准差:Dξ的算术平方根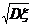 叫做随机变量ξ的标准差,记作
叫做随机变量ξ的标准差,记作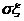
(2)方差的性质: D(aξ+b)=a2Dξ; Dξ=E(ξ2)-(Eξ)2
(3)方差的求法步骤:
①求分布列; ②求期望; ③由公式计算方差。
随机变量的方差与标准差都反映了:随机变量取值的稳定与波动、集中与离散的程度。
2.方差及计算方法
(1)对于一组数据x1,x2,…,xn,
s2=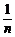 [(x1-
[(x1-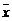 )2+(x2-
)2+(x2-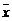 )2+…+(xn-
)2+…+(xn-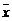 )2]
)2]
叫做这组数据的方差,而s叫做标准差.
(2)方差公式: s2=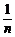 [(x12+x22+…+xn2)-n
[(x12+x22+…+xn2)-n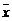 2]
2]
(3)当数据x1,x2,…,xn中各值较大时,可将各数据减去一个适当的常数a,得到x1′=x1-a,x2′=x2-a,…,xn′=xn-a
则s2=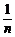 [(x1′2+x2′2+…+xn′2)-n
[(x1′2+x2′2+…+xn′2)-n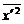 ]
]
1.平均数及计算方法
(1)对于n个数据x1,x2,…,xn,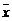 =
=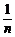 (x1+x2+…+xn)叫做这n个数据的平均数,
(x1+x2+…+xn)叫做这n个数据的平均数,
(2)当数据x1,x2,…,xn的数值较大时,可将各数据同时减去一个适当的常数a,得到x1′=x1-a,x2′=x2-a,…,xn′=xn-a,那么,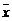 =
=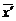 +a.
+a.
(3)如果在n个数据中,x1出现f1次,x2出现f2次,…,xk出现fk次(f1+f2+…+fk=n),那么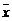 =
=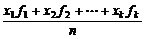 ,叫加权平均数.
,叫加权平均数.
了解离散型随机变量的期望值、方差的意义,会根据离散型随机变量的分布列求出期望值、方差.
(三)解答题:
6、(07上海19)已知函数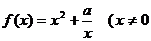 ,常数
,常数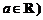 .
.
(1)讨论函数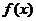 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(2)若函数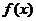 在
在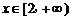 上为增函数,求
上为增函数,求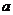 的取值范围.
的取值范围.
解:(1)当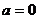 时,
时,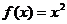 ,
,
对任意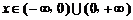 ,
,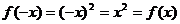 ,
, 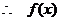 为偶函数.
为偶函数.
当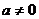 时,
时,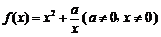 ,
,
取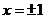 ,得
,得 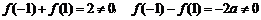 ,
,
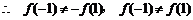 ,
,
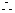 函数
函数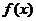 既不是奇函数,也不是偶函数.
既不是奇函数,也不是偶函数.
(2)解法一:设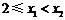 ,
,
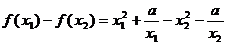
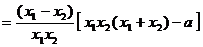 ,
,
要使函数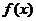 在
在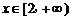 上为增函数,必须
上为增函数,必须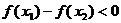 恒成立.
恒成立.
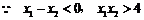 ,即
,即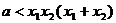 恒成立.
恒成立.
又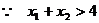 ,
,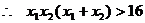 .
.
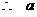 的取值范围是
的取值范围是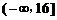 .
.
解法二:当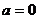 时,
时,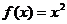 ,显然在
,显然在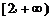 为增函数.
为增函数.
当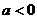 时,反比例函数
时,反比例函数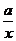 在
在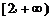 为增函数,
为增函数,
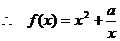 在
在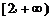 为增函数.
为增函数.
当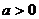 时,同解法一.
时,同解法一.
7、(06湖南20)对1个单位质量的含污物体进行清洗,
清洗前其清洁度(含污物体的清洁度定义为: 为
为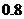 , 要求清洗完后的清洁度为
, 要求清洗完后的清洁度为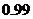 . 有两种方案可供选择, 方案甲: 一次清洗; 方案乙: 分两次清洗. 该物体初次清洗后受残留水等因素影响, 其质量变为
. 有两种方案可供选择, 方案甲: 一次清洗; 方案乙: 分两次清洗. 该物体初次清洗后受残留水等因素影响, 其质量变为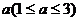 . 设用
. 设用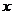 单位质量的水初次清洗后的清洁度是
单位质量的水初次清洗后的清洁度是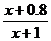
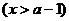 , 用
, 用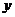 单位质量的水第二次清洗后的清洁度是
单位质量的水第二次清洗后的清洁度是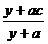 , 其中
, 其中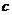
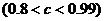 是该物体初次清洗后的清洁度。
是该物体初次清洗后的清洁度。
(Ⅰ)分别求出方案甲以及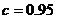 时方案乙的用水量, 并比较哪一种方案用水量较少;
时方案乙的用水量, 并比较哪一种方案用水量较少;
(Ⅱ)若采用方案乙, 当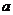 为某固定值时, 如何安排初次与第二次清洗的用水量, 使总用水量最小? 并讨论
为某固定值时, 如何安排初次与第二次清洗的用水量, 使总用水量最小? 并讨论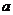 取不同数值时对最少总用水量多少的影响。
取不同数值时对最少总用水量多少的影响。
解: (Ⅰ)设方案甲与方案乙的用水量分别为x与z,由题设有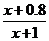 =0.99,解得x=19.
=0.99,解得x=19.
由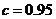 得方案乙初次用水量为3, 第二次用水量y满足方程:
得方案乙初次用水量为3, 第二次用水量y满足方程:
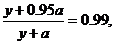 解得y=4
解得y=4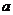 ,故z=4
,故z=4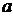 +3.即两种方案的用水量分别为19与4
+3.即两种方案的用水量分别为19与4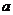 +3.
+3.
因为当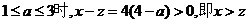 ,故方案乙的用水量较少.
,故方案乙的用水量较少.
(II)设初次与第二次清洗的用水量分别为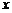 与
与 ,类似(I)得
,类似(I)得
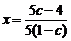 ,
,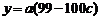 (*)
(*)
于是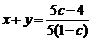 +
+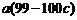
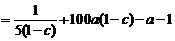
当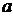 为定值时,
为定值时,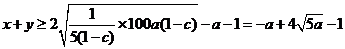 ,
,
当且仅当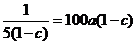 时等号成立.此时
时等号成立.此时
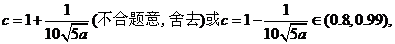
将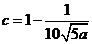 代入(*)式得
代入(*)式得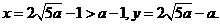
故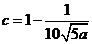 时总用水量最少, 此时第一次与第二次用水量分别为
时总用水量最少, 此时第一次与第二次用水量分别为
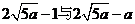 , 最少总用水量是
, 最少总用水量是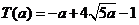 .
.
当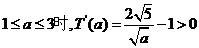 ,故T(
,故T(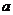 )是增函数(也可以用二次函数的单调性判断).这说明,随着
)是增函数(也可以用二次函数的单调性判断).这说明,随着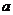 的值的最少总用水量, 最少总用水量最少总用水量.
的值的最少总用水量, 最少总用水量最少总用水量.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com