
4.设一次试验成功的概率为p,进行100次独立重复试验,当p=________时,成功次数的标准差的值最大,其最大值为________.
3.设ξ是随机变量,a、b是非零常数,则下列等式中正确的是 ( )
A.D(aξ+b)=a2Dξ+b B.E(aξ)=a2Eξ
C.D(aξ)=a2Dξ D.E(aξ+b)=aξ
[填空题]
4.二项分布的期望与方差:若ξ-B(n,p),则Eξ=np,Dξ=np(1-p).
同步练习 10.9离散型随机变量的期望与方差
[选择题]
1.下面说法中正确的是 ( )
A.离散型随机变量ξ的期望Eξ反映了ξ取值的概率的平均值。
B.离散型随机变量ξ的方差Dξ反映了ξ取值的平均水平。
C.离散型随机变量ξ的期望Eξ反映了ξ取值的平均水平。
D.离散型随机变量ξ的方差Dξ反映了ξ取值的概率的平均值。
2.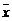 是x1,x2,…,x100的平均数,a是x1,x2,…,x40的平均数,b是x41,x42,…,x100的平均数,则下列各式正确的是 ( )
是x1,x2,…,x100的平均数,a是x1,x2,…,x40的平均数,b是x41,x42,…,x100的平均数,则下列各式正确的是 ( )
A.=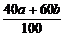 B.
B.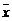 =
=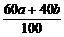 C.
C.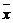 =a+b D
=a+b D
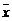 =
=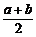
3.离散型随机变量的期望和方差的计算公式与运算性质:
2.求期望与方差.首先应先求出分布列,再代公式求期望与方差.
1.离散型随机变量的期望和方差的意义.
[例1] (1)一枚骰子的六个面上标有1、2、3、4、5、6,投掷一次,向上面的点数为ξ,求Eξ、E(2ξ+3)和Dξ。
(2) 若随机变量ξ的分布列为P(ξ=k)= 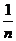 (k=1,2,3,…,n),求Eξ和Dξ。
(k=1,2,3,…,n),求Eξ和Dξ。
(3)一次英语测验由50道选择题构成,每道有4个选项,其中有且仅有一个是正确的,每个选对得3分,选错或不选均不得分,满分150分,某学生选对每一道题的概率为0.7,求该生在这次测验中的成绩的期望与方差。
解:(1)Eξ=x1P1+x2P2+x3P3+…+x6P6=1×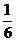 +2×
+2×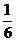 +3×
+3×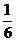 +…+6×
+…+6×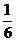 =3.5
=3.5
E(2ξ+3)=2Eξ+3=10
Dξ=(x1-Eξ)2P1+(x2-Eξ)2P2+…+(x6-Eξ)2P6
=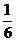 [(1-3.5)2+(2-3.5)2+…(6-3.5)2]=17.5×
[(1-3.5)2+(2-3.5)2+…(6-3.5)2]=17.5×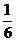 =2.92
=2.92
(2) Eξ=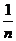 (1+2+…+n)=
(1+2+…+n)=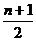
Dξ=Eξ2-(Eξ)2=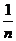 (n2-1)
(n2-1)
(3)设ξ为该生选对试题个数,η为成绩。则ξ-B(50,0.7),η=3ξ
∴Eξ=50×0.7=35;Dξ=50×0.7×0.3=10.5
故Eη=E(3ξ)=3Eξ=105
Dη=D(3ξ)=9Dξ=94.5
[例2](2006年安徽)在添加剂的搭配使用中,为了找到最佳的搭配方案,需要对各种不同的搭配方式作比较。在试制某种牙膏新品种时,需要选用两种不同的添加剂,现有芳香度分别为0,1,2,3,4,5的六种添加剂可供选用。根据试验设计学原理,通常首先要随机选取两种不同的添加剂进行搭配试验。用ξ表示所选用的两种不同的添加剂的芳香度之和,
(Ⅰ)写出ξ的分布列;(以列表的形式给出结论,不必写计算过程).
(Ⅱ)求ξ的数学期望Eξ.(要求写出计算过程或说明道理).
解:(I)ξ的分布列为
|
ξ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
P |
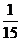 |
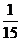 |
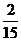 |
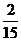 |
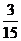 |
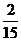 |
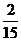 |
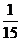 |
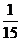 |
(II)由ξ的定义得
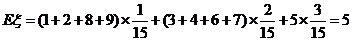 .
.
[例3](2006山东)袋中装着标有数字1,2,3,4,5的小球各2个,从袋中任取3个小球,按3个小球上最大数字的9倍计分,每个小球被取出的可能性都相等。用ξ表示取出的3个小球上的最大数字,求:
(1)取出的3个小球上的数字互不相同的概率;
(2)随机变量ξ的概率分布和数学期望;
(3)计分介于20分到40分之间的概率。
解:(I)解法一:“一次取出的3个小球上的数字互不相同”的事件记为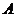 ,
,
则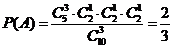
解法二:“一次取出的3个小球上的数字互不相同的事件记为A”,“一次取出的3个小球上有两个数字相同”的事件记为B,则事件A和事件B是互斥事件,因为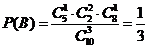 , 所以
, 所以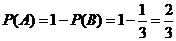 .
.
(II)由题意ξ有可能的取值为:2,3,4,5.
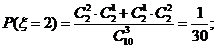
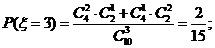
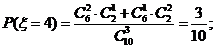
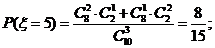
所以随机变量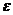 的概率分布为
的概率分布为
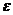 |
2 |
3 |
4 |
5 |
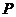 |
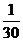 |
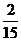 |
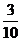 |
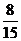 |
因此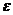 的数学期望为
的数学期望为
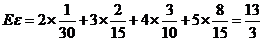
(Ⅲ)“一次取球所得计分介于20分到40分之间”的事件记为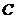 ,则
,则
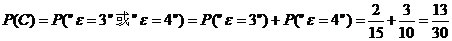
[例4](2006全国Ⅱ)某批产品成箱包装,每箱5件。一用户在购进该批产品前先取出3箱,再从每箱中任意抽取2件产品进行检验。设取出的第一、二、三箱中分别有0件、1件、2件二等品,其余为一等品。
(Ⅰ)用ξ表示抽检的6件产品中二等品的件数,求ξ的分布列及ξ的数学期望;
(Ⅱ)若抽检的6件产品中有2件或2件以上二等品,用户就拒绝购买这批产品,求这批产品给用户拒绝购买的概率。
解:(I)ξ可能的取值为0,1,2,3.
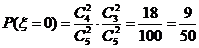 ,
,
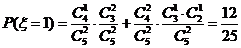 ,
,
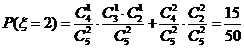 ,
,
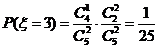 .
.
ξ的分布列为
|
ξ |
0 |
1 |
2 |
3 |
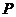 |
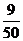 |
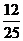 |
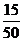 |
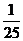 |
数学期望为Eξ=1.2.
(II)所求的概率为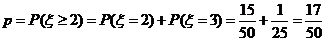
[研讨.欣赏](2006辽宁)现有甲、乙两个项目,对甲项目每投资十万元,一年后利润是1.2万元、1.18万元、1.17万元的概率分别为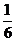 、
、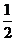 、
、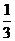 ;已知乙项目的利润与产品价格的调整有关,在每次调整中价格下降的概率都是
;已知乙项目的利润与产品价格的调整有关,在每次调整中价格下降的概率都是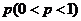 ,设乙项目产品价格在一年内进行2次独立的调整,记乙项目产品价格在一年内的下降次数为ξ,对乙项目每投资十万元, ξ取0、1、2时, 一年后相应利润是1.3万元、1.25万元、0.2万元.随机变量ξ1、ξ2分别表示对甲、乙两项目各投资十万元一年后的利润.
,设乙项目产品价格在一年内进行2次独立的调整,记乙项目产品价格在一年内的下降次数为ξ,对乙项目每投资十万元, ξ取0、1、2时, 一年后相应利润是1.3万元、1.25万元、0.2万元.随机变量ξ1、ξ2分别表示对甲、乙两项目各投资十万元一年后的利润.
(I)求ξ1、ξ2的概率分布和数学期望Eξ1、Eξ2;
(II)当Eξ1<Eξ2时,求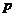 的取值范围.
的取值范围.
解(I)法一:ξ1的概率分布为
|
ξ1 |
1.2 |
1.18 |
1.17 |
|
P |
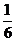 |
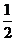 |
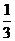 |

由题设的ξ-B(2,p),即ξ的概率分布为
|
ξ |
0 |
1 |
2 |
|
P |
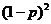 |
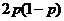 |
 |
故ξ2的概率分布为
|
ξ2 |
1.3 |
1.25 |
0.2 |
|
P |
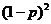 |
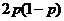 |
 |
所以ξ2的数学期望为
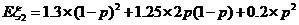
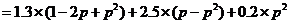
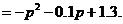
解法二:ξ1的概率分布为
|
ξ1 |
1.2 |
1.18 |
1.17 |
|
P |
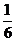 |
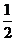 |
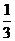 |

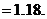
设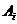 表示事件“第 i 次调整,价格下降”(i=1,2),则
表示事件“第 i 次调整,价格下降”(i=1,2),则

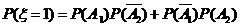
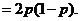
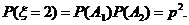
故ξ2的概率分布为
|
ξ2 |
1.3 |
1.25 |
0.2 |
|
P |
(1-p)2 |
2p(1-p) |
P2 |
所以ξ2的数学
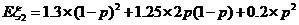
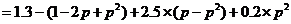
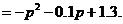
(II)解:由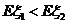 ,得
,得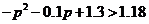 ,
,
整理得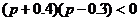 ,
,
解得 。
。
因为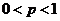 ,所以,当
,所以,当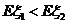 时,
时,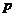 得取值范围是
得取值范围是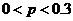 。
。
6.包装的重量的平均水平一样,甲机包装重量的差别大,不稳定,答案:乙
4.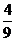 ; 5.
; 5.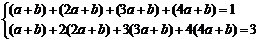
得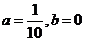 ,∴
,∴ 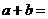
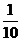 .
.
3. P(ξ=0)=0.43,P(ξ=1)=0.6×0.42,P(ξ=2)=0.6×0.4,P(ξ=3)=0.6,Eξ=2.376;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com