
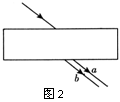
2. 如图2所示,一束平行光射到平行玻璃板上,经过上、下两个表面折射后,分成a、b两束单色光射出平行玻璃板,以下说法中正确的是( )
A.a的折射率大于b的折射率
B.a的频率小于b的频率
C.由于玻璃对a、b两束单色光的折射率不同,所以它们不平行
D.若单色光a照射某种金属时发生光电效应,则单色光b照射该金属时一定发生光电效应
1.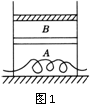 如图1所示,一个与外界绝热的气缸有一个绝热的活塞,中间有一个固定的导热性良好的隔板,封闭着两部分气体A和B,活塞处于静止平衡状态,现通过电热丝对A气体加热一段时间,后来活塞达到新的静止平衡状态,不计气体分子势能,不计活塞与气缸壁的摩擦,大气压强保持不变,则( )
如图1所示,一个与外界绝热的气缸有一个绝热的活塞,中间有一个固定的导热性良好的隔板,封闭着两部分气体A和B,活塞处于静止平衡状态,现通过电热丝对A气体加热一段时间,后来活塞达到新的静止平衡状态,不计气体分子势能,不计活塞与气缸壁的摩擦,大气压强保持不变,则( )
A.气体A吸热,内能增加
B.气体B吸热,对外做功,内能不变
C.气体A分子单位时间内对器壁单位面积碰撞次数增多
 D.气体B分子单位时间内对器壁单位面积碰撞次数不变
D.气体B分子单位时间内对器壁单位面积碰撞次数不变
21.(本小题满分14分)
已知数列 的前n项和为
的前n项和为 ,且
,且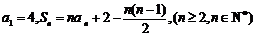
(1)求数列 的通项公式;
的通项公式;
(2)设数列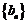 满足:
满足: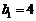 ,且
,且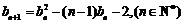 ,
,
求证: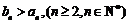 ;
;
(3)求证: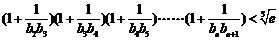 。
。
解:(1)当 时,
时,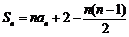 ,
,
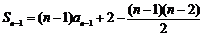 ,可得:
,可得: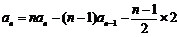 ,
, 

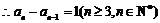 .
.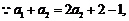
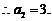
可得,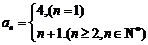
(2)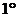 当
当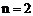 时,
时,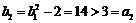 ,不等式成立.
,不等式成立.
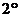 假设当
假设当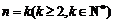 时,不等式成立,即
时,不等式成立,即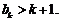 那么,当
那么,当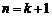 时,
时,
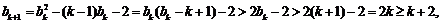
所以当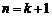 时,不等式也成立。
时,不等式也成立。
根据(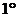 ),(
),(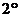 )可知,当
)可知,当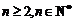 时,
时,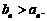
(3)设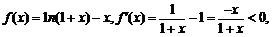
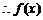 在
在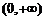 上单调递减,
上单调递减,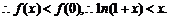
∵当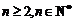 时,
时,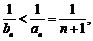


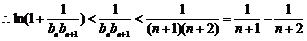 ,
,
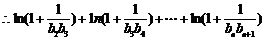
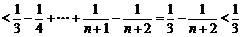

20.解析:(1)
∵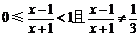 ,∴函数
,∴函数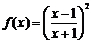 的值域为
的值域为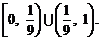
由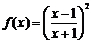 ,得
,得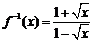 ,因此,函数
,因此,函数 的反函数
的反函数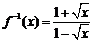
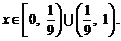
(2) ,当且仅当
,当且仅当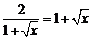 ,
,
即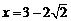 时,
时,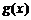 有最小值
有最小值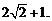
(3)由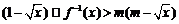 ,得
,得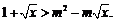
设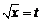 ,则
,则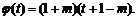
根据题意,对区间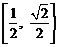 中的一切t值,
中的一切t值,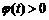 恒成立.
恒成立.
则 得
得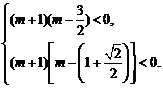 ∴
∴


∴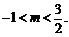 即实数m的取值范围是
即实数m的取值范围是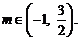
20.(本小题满分13分)已知函数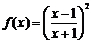 (其中x≥1).
(其中x≥1). 

(1)求函数 的反函数
的反函数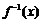 ;
;
(2)设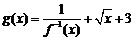 ,求函数
,求函数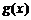 最小值及相应的x值;
最小值及相应的x值;
(3)若不等式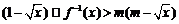 对于区间
对于区间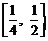 上的每一个x值都成立,求实数m的取值范围.
上的每一个x值都成立,求实数m的取值范围.
19.解析:(1)由题知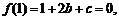
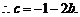
记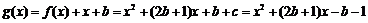 ,
,
则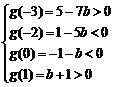
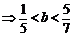 ,
即
,
即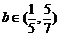 .
. 

(2)令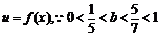 ,
,
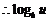 在区间
在区间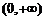 上是减函数.
上是减函数.
而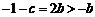 ,函数
,函数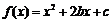 的对称轴为
的对称轴为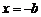 ,
,
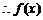 在区间
在区间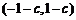 上单调递增.
上单调递增.
从而函数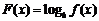 在区间
在区间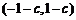 上为减函数.
上为减函数.
且 在区间
在区间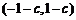 上恒有
上恒有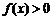 ,只需要
,只需要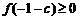 ,
,
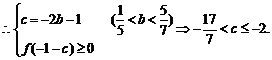
19.(本小题满分12分)已知二次函数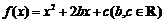 满足
满足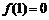 ,且关于
,且关于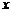 的方程
的方程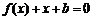 的两个实数根分别在区间
的两个实数根分别在区间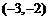 、
、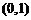 内.
内.
(1)求实数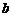 的取值范围;
的取值范围;
(2)若函数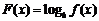 在区间
在区间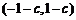 上具有单调性,求实数
上具有单调性,求实数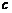 的取值范围.
的取值范围.
18.解:(1)设前n个月投资总额为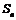 ,
,
则 时,
时,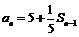 ,∴
,∴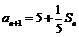 ,
,
两式相减得: ,∴
,∴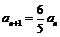 ,
,


又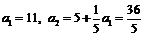 ,∴
,∴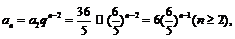
又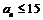 ,∴
,∴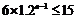 ,∴
,∴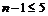 ,∴
,∴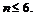
∴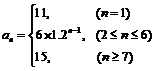
(2)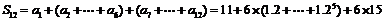
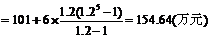
故预计2010年全年共需投资154.64万元.
18.(本题满分12分)某企业为了适应市场需求,计划从2010年元月起,在每月固定投资5万元的基础上,元月份追加投资6万元,以后每月的追加投资额均为之前几个月投资额总和的20%,但每月追加部分最高限额为10万元. 记第n个月的投资额为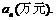
(1)求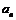 与n的关系式;
与n的关系式;
(2)预计2010年全年共需投资多少万元?(精确到0.01,参考数据: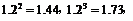
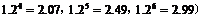
17.解:(1)由题设知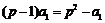 ,解得
,解得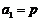 。
。
由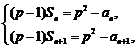 两式作差得
两式作差得
所以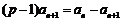 ,即
,即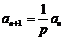 ,
,
可见,数列 是首项为
是首项为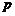 ,公比为
,公比为 的等比数列。
的等比数列。
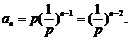
(2)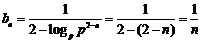 .
. 

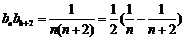
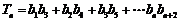
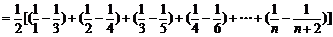
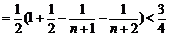 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com