
5.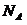 表示阿伏加德罗常数的值,下列说法正确的是
表示阿伏加德罗常数的值,下列说法正确的是
A.标准状况下,22.4L二氯甲烷的分子数约为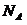 个
个
B.盛有 的密闭容器中含有
的密闭容器中含有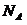 个氧原子,则
个氧原子,则 的物质的量为0.5mol
的物质的量为0.5mol
C.17.6g丙烷中所含的极性共价键为 个
个
D.电解精炼铜时,若阴极得到电子数为 个,则阳极质量减少64g
个,则阳极质量减少64g
4.NA表示阿伏加德罗常数,下列叙述正确的是
 A.等物质的量的N2和CO所含分子数均为NA B.1.7g
H2O2中含有的电子数为0.9 NA
A.等物质的量的N2和CO所含分子数均为NA B.1.7g
H2O2中含有的电子数为0.9 NA
C.1mol Na2O2 固体中含离子总数为4 NA D.标准状况下,2.24L戊烷所含分子数为0.1 NA
3.设NA 代表阿伏加德罗常数(NA )的数值,下列说法正确的是
A.1 mol 硫酸钾中阴离子所带电荷数为NA
B.乙烯和环丙烷(C3H6 )组成的28g混合气体中含有3NA 个氢原子
C.标准状况下,22.4L氯气与足量氢氧化钠溶液反应转移的电子数为NA
D.将0.1mol氯化铁溶于1L水中,所得溶液含有0.1NA Fe3+
2.  和
和 是氧元素的两种
是氧元素的两种 核素,
核素, 表示阿伏伽德罗常数,下列说法正确的是
表示阿伏伽德罗常数,下列说法正确的是
A. 与
与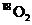 互为同分异构体
B.
互为同分异构体
B.  与
与 核外电子排布方式不同
核外电子排布方式不同
C.通过化学变化可以实现 与
与 间的相互转化
间的相互转化
D.标准状况下,1.12L 和1.12L
和1.12L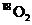 均含有0.1
均含有0.1 个氧原子
个氧原子
1.设  为阿伏加德罗常数的数值,
为阿伏加德罗常数的数值, 下列说法正确的是
下列说法正确的是
A.16g  中含有4
中含有4 个C-H键 B.1mol·
个C-H键 B.1mol·
 溶液含有
溶液含有 个
个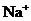
C.1mol
Cu和足量稀硝酸反应产生  个NO分子
个NO分子
D.常温常压下,22.4L
 中含有
中含有  个
个 分子
分子
2.已知下列不等式,比较正数m、n的大小:
(1) m<
m< n
(2)
n
(2)  m>
m> n
n
(3) 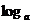 m<
m<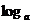 n(0<a<1) (4)
n(0<a<1) (4)
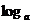 m>
m>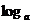 n(a>1)
n(a>1)
解:(1)考查函数y= x
x
∵3>1,∴函数y= x在(0,+∞)是增函数
x在(0,+∞)是增函数
∵ m<
m< n,∴m<n
n,∴m<n
(2)考查函数y= x
x
∵0<0.3<1,∴函数y= x在(0,+∞)上是减函数
x在(0,+∞)上是减函数
∵ m>
m> n,
n,
∴m<n
(3)考查函数y=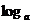 x
x
∵0<a<1,
∴函数y=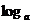 x在(0,+∞)上是减函数
x在(0,+∞)上是减函数
∵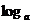 m<
m<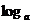 n,
n,
∴m>n
(4)考查函数y=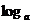 x
x
∵a>1,
∴函数y=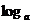 x在(0,+∞)上是增函数
x在(0,+∞)上是增函数
∵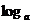 m>
m>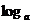 n,
n,
∴m>n
1.比较 0.7与
0.7与 0.8两值大小
0.8两值大小
解:考查函数y=log2x
∵2>1,∴函数y= x在(0,+∞)上是增函数
x在(0,+∞)上是增函数
又0.7<1,∴ 0.7<
0.7< 1=0
1=0
再考查函数y= x
x
∵0< <1
<1
∴函数y= x在(0,+∞)上是减函数
x在(0,+∞)上是减函数
又1>0.8,∴ 0.8>
0.8> 1=0
1=0
∴ 0.7<0<
0.7<0< 0.8
0.8
∴ 0.7<
0.7< 0.8
0.8
比较对数大小的方法,两种情况,求函数定义值域的方法
⑴
⑵
⑶
例1比较下列各组数中两个值的大小:
⑴ ;
⑵
;
⑵ ;
;
⑶
解:⑴考查对数函数 ,因为它的底数2>1,所以它在(0,+∞)上是增函数,于是
,因为它的底数2>1,所以它在(0,+∞)上是增函数,于是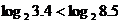
⑵考查对数函数 ,因为它的底数0<0.3<1,所以它在(0,+∞)上是减函数,于是
,因为它的底数0<0.3<1,所以它在(0,+∞)上是减函数,于是
小结1:两个同底数的对数比较大小的一般步骤:
①确定所要考查的对数函数;
②根据对数底数判断对数函数增减性;
③比较真数大小,然后利用对数函数的增减性判断两对数值的大小
⑶当 时,
时, 在(0,+∞)上是增函数,于是
在(0,+∞)上是增函数,于是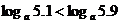
当 时,
时,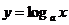 在(0,+∞)上是减函数,于是
在(0,+∞)上是减函数,于是
小结2:分类讨论的思想
对数函数的单调性取决于对数的底数是大于1还是小于1而已知条件并未指明,因此需要对底数 进行讨论,体现了分类讨论的思想,要求学生逐步掌握
进行讨论,体现了分类讨论的思想,要求学生逐步掌握
例3比较下列各组中两个值的大小:
⑴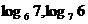 ;
⑵
;
⑵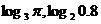
分析:由于两个对数值不同底,故不能直接比较大小,可在两对数值中间插入一个已知数,间接比较两对数的大小
解:⑴ ,
,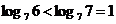 ,
,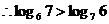
⑵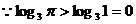 ,
, ,
, ;
;
小结3:引入中间变量比较大小
例3仍是利用对数函数的增减性比较两个对数的大小,当不能直接比较时,经常在两个对数中间插入1或0等,间接比较两个对数的大小
例4 求下列函数的定义域、值域:
⑴ ⑵
⑵
⑶ ⑷
⑷

解:⑴要使函数有意义,则须:
 即:
即:
∵ ∴
∴ 从而
从而 
∴ ∴
∴ ∴
∴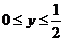
∴定义域为[-1,1],值域为
⑵∵ 对一切实数都恒成立
对一切实数都恒成立
∴函数定义域为R
从而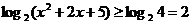 即函数值域为
即函数值域为
⑶要使函数有意义,则须:

由 ∴在此区间内
∴在此区间内
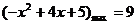
∴ 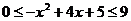
从而  即:值域为
即:值域为
∴定义域为[-1,5],值域为
⑷要使函数有意义,则须:
由①:
由②:∵ 时
则须
时
则须  ,
,
综合①②得 
当 时
时  ∴
∴
∴ ∴
∴ 
∴定义域为(-1,0),值域为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com