
函数思想的实质就是用联系与变化的观点提出数学对象,抽象数量特征,建立函数关系,求得问题的解决 纵观近几年高考题,考查函数思想方法尤其是应用题力度加大,因此一定要认识函数思想实质,强化应用意识
纵观近几年高考题,考查函数思想方法尤其是应用题力度加大,因此一定要认识函数思想实质,强化应用意识
典型题例示范讲解
例1设f(x)是定义在R上的偶函数,其图象关于直线x=1对称,对任意x1、x2∈[0, ],都有f(x1+x2)=f(x1)·f(x2),且f(1)=a>0
],都有f(x1+x2)=f(x1)·f(x2),且f(1)=a>0
(1)求f( )、f(
)、f(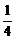 );
);
(2)证明f(x)是周期函数;
(3)记an=f(2n+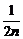 ),求
),求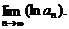
命题意图 本题主要考查函数概念,图象函数的奇偶性和周期性以及数列极限等知识,还考查运算能力和逻辑思维能力
本题主要考查函数概念,图象函数的奇偶性和周期性以及数列极限等知识,还考查运算能力和逻辑思维能力
知识依托 认真分析处理好各知识的相互联系,抓住条件f(x1+x2)=
认真分析处理好各知识的相互联系,抓住条件f(x1+x2)=
f(x1)·f(x2)找到问题的突破口
错解分析 不会利用f(x1+x2)=f(x1)·f(x2)进行合理变形
不会利用f(x1+x2)=f(x1)·f(x2)进行合理变形
技巧与方法 由f(x1+x2)=f(x1)·f(x2)变形为
由f(x1+x2)=f(x1)·f(x2)变形为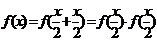 是解决问题的关键
是解决问题的关键
(1)
解 因为对x1,x2∈[0,
因为对x1,x2∈[0, ],都有f(x1+x2)=f(x1)·f(x2),所以f(x)=
],都有f(x1+x2)=f(x1)·f(x2),所以f(x)=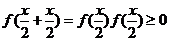 , x∈[0,1]
, x∈[0,1]
又因为f(1)=f( +
+ )=f(
)=f( )·f(
)·f( )=[f(
)=[f( )]2
)]2
f( )=f(
)=f(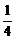 +
+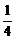 )=f(
)=f(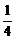 )·f(
)·f(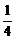 )=[f(
)=[f(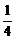 )]2
)]2
又f(1)=a>0
∴f( )=a
)=a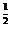 , f(
, f(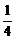 )=a
)=a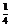
(2)证明 依题意设y=f(x)关于直线x=1对称,故f(x)=f(1+1-x),
依题意设y=f(x)关于直线x=1对称,故f(x)=f(1+1-x),
即 f(x)=f(2-x),x∈R
又由f(x)是偶函数知 f(-x)=f(x),x∈R
∴f(-x)=f(2-x),x∈R
将上式中-x以x代换得f(x)=f(x+2),这表明f(x)是R上的周期函数,且2是它的一个周期
(3)解 由(1)知f(x)≥0,x∈[0,1]
由(1)知f(x)≥0,x∈[0,1]
∵f( )=f(n·
)=f(n·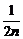 )=f(
)=f(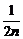 +(n-1)
+(n-1) 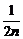 )=f(
)=f(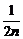 )·f((n-1)·
)·f((n-1)·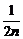 )=……
)=……
=f(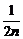 )·f(
)·f(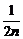 )·……·f(
)·……·f(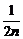 )
)
=[f(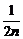 )]n=a
)]n=a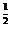
∴f(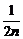 )=a
)=a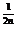

又∵f(x)的一个周期是2
∴f(2n+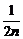 )=f(
)=f(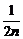 ),
),
∴an=f(2n+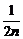 )=f(
)=f(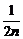 )=a
)=a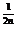

因此an=a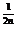
∴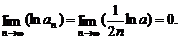
例2甲、乙两地相距S千米,汽车从甲地匀速驶到乙地,速度不得超过c千米/小时,已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成,可变部分与速度v(km/h)的平方成正比,比例系数为b,固定部分为a元
(1)把全程运输成本y(元)表示为v(km/h)的函数,并指出这个函数的定义域;
(2)为了使全程运输成本最小,汽车应以多大速度行驶?
命题意图 本题考查建立函数的模型、不等式性质、最值等知识,还考查学生综合运用所学数学知识解决实际问题的能力
本题考查建立函数的模型、不等式性质、最值等知识,还考查学生综合运用所学数学知识解决实际问题的能力
知识依托 运用建模、函数、数形结合、分类讨论等思想方法
运用建模、函数、数形结合、分类讨论等思想方法
错解分析 不会将实际问题抽象转化为具体的函数问题,易忽略对参变量的限制条件
不会将实际问题抽象转化为具体的函数问题,易忽略对参变量的限制条件
技巧与方法 四步法
四步法 (1)读题;(2)建模;(3)求解;(4)评价
(1)读题;(2)建模;(3)求解;(4)评价
解法一 (1)依题意知,汽车从甲地匀速行驶到乙地所用时间为
(1)依题意知,汽车从甲地匀速行驶到乙地所用时间为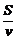 ,全程运输成本为y=a·
,全程运输成本为y=a·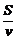 +bv2·
+bv2·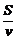 =S(
=S(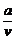 +bv)
+bv)
∴所求函数及其定义域为y=S(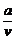 +bv),v∈(0,c
+bv),v∈(0,c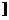

(2)依题意知,S、a、b、v均为正数
∴S(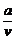 +bv)≥2S
+bv)≥2S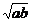 ①
①
当且仅当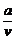 =bv,即v=
=bv,即v=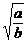 时,①式中等号成立
时,①式中等号成立
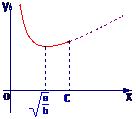
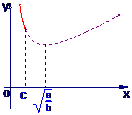
若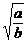 ≤c则当v=
≤c则当v=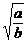 时,有ymin=2S
时,有ymin=2S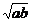 ;
;
若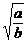 >c,则当v∈(0,c
>c,则当v∈(0,c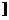 时,有S(
时,有S(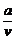 +bv)-S(
+bv)-S(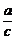 +bc)
+bc)
=S[(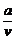 -
-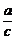 )+(bv-bc)]=
)+(bv-bc)]=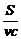 (c-v)(a-bcv)
(c-v)(a-bcv)
∵c-v≥0,且c>bc2, ∴a-bcv≥a-bc2>0
∴S(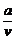 +bv)≥S(
+bv)≥S(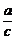 +bc),当且仅当v=c时等号成立,
+bc),当且仅当v=c时等号成立,
也即当v=c时,有ymin =S(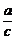 +bc);
+bc);
综上可知,为使全程运输成本y最小,当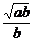 ≤c时,行驶速度应为v=
≤c时,行驶速度应为v=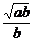 , 当
, 当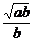 >c时行驶速度应为v=c
>c时行驶速度应为v=c
解法二 (1)同解法一
(1)同解法一
(2)∵函数y=S(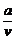 +bv), v∈(0,+∞),
+bv), v∈(0,+∞),
当x∈(0,
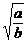 )时,y单调减小,
)时,y单调减小,
当x∈(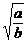 ,+∞)时y单调增加,
,+∞)时y单调增加,
当x=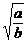 时y取得最小值,而全程运输成本函数为y=Sb(v+
时y取得最小值,而全程运输成本函数为y=Sb(v+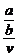 ),v∈(0,c
),v∈(0,c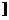

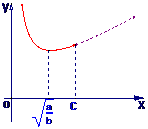

∴当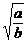 ≤c时,则当v=
≤c时,则当v=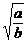 时,y最小,若
时,y最小,若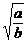 >c时,则当v=c时,y最小
>c时,则当v=c时,y最小 结论同上
结论同上
例3 设函数f(x)的定义域为R,对任意实数x、y都有f(x+y)=f(x)+f(y),当x>0时f(x)<0且f(3)=-4
(1)求证 f(x)为奇函数;
f(x)为奇函数;
(2)在区间[-9,9]上,求f(x)的最值
(1)证明 令x=y=0,得f(0)=0
令x=y=0,得f(0)=0
令y=-x,得f(0)=f(x)+f(-x),即f(-x)=-f(x)
∴f(x)是奇函数
(2)解 1°,任取实数x1、x2∈[-9,9]且x1<x2,这时,x2-x1>0,
1°,任取实数x1、x2∈[-9,9]且x1<x2,这时,x2-x1>0,
f(x1)-f(x2)=f[(x1-x2)+x2]-f(x2)=f(x1-x2)+f(x2)-f(x1)=-f(x2-x1)
因为x>0时f(x)<0,∴f(x1)-f(x2)>0
∴f(x)在[-9,9]上是减函数
故f(x)的最大值为f(-9),最小值为f(9)
而f(9)=f(3+3+3)=3f(3)=-12,f(-9)=-f(9)=12
∴f(x)在区间[-9,9]上的最大值为12,最小值为-12
学生巩固练习
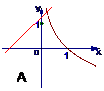
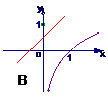
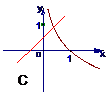
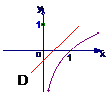
1 函数y=x+a与y=logax的图象可能是( )
函数y=x+a与y=logax的图象可能是( )
2 定义在区间(-∞,+∞)的奇函数f(x)为增函数,偶函数g(x)在区间[0,+∞)的图象与f(x)的图象重合,设a>b>0,给出下列不等式
定义在区间(-∞,+∞)的奇函数f(x)为增函数,偶函数g(x)在区间[0,+∞)的图象与f(x)的图象重合,设a>b>0,给出下列不等式
①f(b)-f(-a)>g(a)-g(-b) ②f(b)-f(-a)<g(a)-g(-b)
③f(a)-f(-b)>g(b)-g(-a) ④f(a)-f(-b)<g(b)-g(-a)
其中成立的是( )
A ①与④ B
①与④ B ②与③ C
②与③ C ①与③ D
①与③ D ②与④
②与④
3 若关于x的方程22x+2xa+a+1=0有实根,则实数a的取值范围是____
若关于x的方程22x+2xa+a+1=0有实根,则实数a的取值范围是____
4 设a为实数,函数f(x)=x2+|x-a|+1,x∈R
设a为实数,函数f(x)=x2+|x-a|+1,x∈R
(1)讨论f(x)的奇偶性;(2)求f(x)的最小值
5 设f(x)=
设f(x)=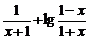

(1)证明 f(x)在其定义域上的单调性;
f(x)在其定义域上的单调性;
(2)证明 方程f-1(x)=0有惟一解;
方程f-1(x)=0有惟一解;
(3)解不等式f[x(x- )]<
)]<

6 定义在(-1,1)上的函数f(x)满足①对任意x、y∈(-1,1),都有f(x)+f(y)=f(
定义在(-1,1)上的函数f(x)满足①对任意x、y∈(-1,1),都有f(x)+f(y)=f(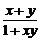 );②当x∈(-1,0)时,有f(x)>0
);②当x∈(-1,0)时,有f(x)>0
求证
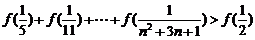

 7
7 某工厂拟建一座平面图(如下图)为矩形且面积为200平方米的三级污水处理池,由于地形限制,长、宽都不能超过16米,如果池外周壁建造单价为每米400元,中间两条隔墙建造单价为每米248元,池底建造单价为每平方米80元(池壁厚度忽略不计,且池无盖)
某工厂拟建一座平面图(如下图)为矩形且面积为200平方米的三级污水处理池,由于地形限制,长、宽都不能超过16米,如果池外周壁建造单价为每米400元,中间两条隔墙建造单价为每米248元,池底建造单价为每平方米80元(池壁厚度忽略不计,且池无盖)
(1)写出总造价y(元)与污水处理池长x(米)的函数关系式,并指出其定义域
(2)求污水处理池的长和宽各为多少时,污水处理池的总造价最低?并求最低总造价
8 已知函数f(x)在(-∞,0)∪(0,+∞)上有定义,且在(0,+∞)上是增函数,f(1)=0,又g(θ)=sin2θ-mcosθ-2m,θ∈[0,
已知函数f(x)在(-∞,0)∪(0,+∞)上有定义,且在(0,+∞)上是增函数,f(1)=0,又g(θ)=sin2θ-mcosθ-2m,θ∈[0,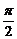 ],设M={m|g(θ)<0,m∈R},N={m|f[g(θ)]<0},求M∩N
],设M={m|g(θ)<0,m∈R},N={m|f[g(θ)]<0},求M∩N
函数图象的几何特征与函数性质的数量特征紧密结合,有效地揭示了各类函数和定义域、值域、单调性、奇偶性、周期性等基本属性,体现了数形结合的特征与方法,为此,既要从定形、定性、定理、定位各方面精确地观察图形、绘制图形,又要熟练地掌握函数图象的平移变换、对称变换
所谓函数观点,实质是将问题放到动态背景上去加以考虑 高考试题涉及5个方面
高考试题涉及5个方面 (1)原始意义上的函数问题;(2)方程、不等式作为函数性质解决;(3)数列作为特殊的函数成为高考热点;(4)辅助函数法;(5)集合与映射,作为基本语言和工具出现在试题中
(1)原始意义上的函数问题;(2)方程、不等式作为函数性质解决;(3)数列作为特殊的函数成为高考热点;(4)辅助函数法;(5)集合与映射,作为基本语言和工具出现在试题中
概念是数学的基础,而函数是数学中最主要的概念之一,函数概念贯穿在中学代数的始终 数、式、方程、函数、排列组合、数列极限等是以函数为中心的代数
数、式、方程、函数、排列组合、数列极限等是以函数为中心的代数 近十年来,高考试题中始终贯穿着函数及其性质这条主线
近十年来,高考试题中始终贯穿着函数及其性质这条主线
4 如图,在函数y=lgx的图象上有A、B、C三点,它们的横坐标分别为m,m+2,m+4(m>1)
如图,在函数y=lgx的图象上有A、B、C三点,它们的横坐标分别为m,m+2,m+4(m>1)
(1)若△ABC面积为S,求S=f(m);
(2)判断S=f(m)的增减性
 5
5 如图,函数y=
如图,函数y=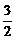 |x|在x∈[-1,1]的图象上有两点A、B,AB∥Ox轴,点M(1,m)(m∈R且m>
|x|在x∈[-1,1]的图象上有两点A、B,AB∥Ox轴,点M(1,m)(m∈R且m>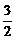 )是△ABC的BC边的中点
)是△ABC的BC边的中点
(1)写出用B点横坐标t表示△ABC面积S的函数解析式S=f(t);
(2)求函数S=f(t)的最大值,并求出相应的C点坐标
6 已知函数f(x)是y=
已知函数f(x)是y=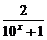 -1(x∈R)的反函数,函数g(x)的图象与函数y=-
-1(x∈R)的反函数,函数g(x)的图象与函数y=-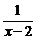 的图象关于y轴对称,设F(x)=f(x)+g(x)
的图象关于y轴对称,设F(x)=f(x)+g(x)
(1)求函数F(x)的解析式及定义域;
(2)试问在函数F(x)的图象上是否存在两个不同的点A、B,使直线AB恰好与y轴垂直?若存在,求出A、B的坐标;若不存在,说明理由
7 已知函数f1(x)=
已知函数f1(x)=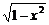 ,f2(x)=x+2,
,f2(x)=x+2,
(1)设y=f(x)=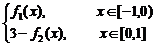 ,试画出y=f(x)的图象并求y=f(x)的曲线绕x轴旋转一周所得几何体的表面积;
,试画出y=f(x)的图象并求y=f(x)的曲线绕x轴旋转一周所得几何体的表面积;
(2)若方程f1(x+a)=f2(x)有两个不等的实根,求实数a的范围
(3)若f1(x)>f2(x-b)的解集为[-1,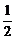 ],求b的值
],求b的值
8 设函数f(x)=x+
设函数f(x)=x+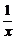 的图象为C1,C1关于点A(2,1)对称的图象为C2,C2对应的函数为g(x)
的图象为C1,C1关于点A(2,1)对称的图象为C2,C2对应的函数为g(x)
(1)求g(x)的解析表达式;
(2)若直线y=b与C2只有一个交点,求b的值,并求出交点坐标;
(3)解不等式logag(x)<loga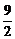 (0<a<1)
(0<a<1)
32. (1)S。 (2)CH4<NH3<H2O; 共价键和离子键; 离子晶体; 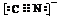 。
。
(3)CO32 -+H2O HCO3- +OH- 或 C2O42 -+H2O
HCO3- +OH- 或 C2O42 -+H2O HC2O4- +OH-。 (4)0.3 mol Na2O2、0.1 mol
Na2CO3
HC2O4- +OH-。 (4)0.3 mol Na2O2、0.1 mol
Na2CO3
31. (1)N≡N;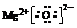 ;第四周期,第VIII族。 (2)①③。 (3)CH4;NH3;NH3+H3O+= NH4+ +H2O。
;第四周期,第VIII族。 (2)①③。 (3)CH4;NH3;NH3+H3O+= NH4+ +H2O。
(4)3SO2+3Ba2++2H2O+2NO3- = 3BaSO4↓+2NO↑+4H+。 SO2。
30.
(1)Mg 1s22s22p6 (2)离子 2F2+2H2O=4HF+O2
(3)b d(B是氧气或氮气)
(4)Na 钠与水反应比镁与反应剧烈后氢扬化钠的碱性比氢氧化镁强(合理即给分)
29.
(1)第三周期 ⅦA (2)2Na+2H2O=2NaOH+H2↑ 大于
(3)大 SiO2是原子晶体 或 小 CO2是分子晶体 (合理即给分)
(4)Cl 高氯酸的酸性大于硫酸的酸性或氯化氢稳定比硫化氢强(合理即给分)
28.
(1)S C
(2)V形 直线形 SO2 因为CO2是非极性分子,SO2和H2O都是极性分子,根据“相似相溶”原理,SO2在H2O中的溶解度较大
(3)Cr 四 +6
(4)F-H…F F-H…O O-H…F O-H…O
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com