
1. 对于已知直线a,如果直线b同时满足下列三个条件: ① 与直线a异面;②
与直线a所成的角为定值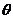 ;③ 与直线a的距离为定值d.那么这样的直线b有
;③ 与直线a的距离为定值d.那么这样的直线b有
A. 1条 B. 2条 C. 3条 D. 无数条
4. 构造几何模型求解
在正方体的8个顶点的所有连线中,有多少对异面直线?
与空间不共面的四点距离相等的平面有多少个?
(05年湖北)以平面六面体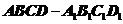 的任意三个顶点为顶点作三角形,从中随机取出两个三角形,则这两个三角形不共面的概率为
的任意三个顶点为顶点作三角形,从中随机取出两个三角形,则这两个三角形不共面的概率为
A. 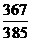 B.
B. 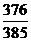 C.
C. 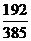 D.
D.
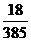 A
A
在知识的网络交汇点初设计命题是近几年高考命题改革强调的重要观念之一,在复习备考中,要把握好知识间的纵横联系和综合,使所学知识真正融会贯通,运用自如,形成有序的网络化知识体系。
3. 结合“立几”图形求解
如果把两条异面直线看作“一对”,那么六棱锥的棱和底面所有的12条直线中,异面直线有
A. 12 B. 24 C. 36 D. 48 B
用正五棱柱的10个顶点中的5个顶点作四棱锥的5个顶点,共可得多少个四棱锥?
分类:以棱柱的底面为棱锥的底面 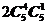 ;
;
以棱柱的侧面为棱锥的底面 
以棱柱的对角面为棱锥的底面
以图中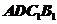 (梯形)为棱锥的底面
(梯形)为棱锥的底面 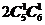
2. 结合“立几”概念求解
例3: 空间10个点无三点共线,其中有6个点共面,此外没有任何四个点共面,则这些点可以组成多少个四棱锥?
解析:
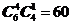
1. 直接求解
例1:从平面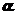 上取6个点,从平面
上取6个点,从平面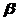 上取4个点,这10个点最多可以确定多少个三棱锥?
上取4个点,这10个点最多可以确定多少个三棱锥?
解析: 利用三棱锥的形成将问题分成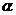 平面上有1个点、2个点、3个点三类直接求解共有
平面上有1个点、2个点、3个点三类直接求解共有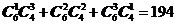 个三棱锥
个三棱锥
例2: 在四棱锥P-ABCD中,顶点为P,从其它的顶点和各棱的中点中取3个,使它们和点P在同一平面上,不同的取法有 A.40 B. 48 C. 56 D. 62种
解析: 满足题设的取法可以分成三类
(1)
在四棱锥的每一个侧面上除P点外取三点有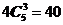 种不同取法;
种不同取法;
(2)
在两个对角面上除点P外任取3点,共有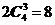 种不同取法;
种不同取法;
(3)
过点P的每一条棱上的3点和与这条棱异面的棱的中点也共面,共有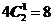 种不同取法,故共有40+8+8=56种
种不同取法,故共有40+8+8=56种
评注:这类问题应根据立体图形的几何特点,选取恰当的分类标准,做到分类不重复、不遗漏。
⑴解有关函数最大值、最小值的实际问题,需要分析问题中各个变量之间的关系,找出适当的函数关系式,并确定函数的定义区间;所得结果要符合问题的实际意义.
⑵根据问题的实际意义来判断函数最值时,如果函数在此区间上只有一个极值点,那么这个极值就是所求最值,不必再与端点值比较.
⑶相当多有关最值的实际问题用导数方法解决较简单
2.在半径为R的圆内,作内接等腰三角形,当底边上高为___时,它的面积最大
答案: 4.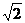 a
a 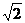 b 5.
b 5.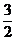 R
R
1.使内接椭圆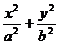 =1的矩形面积最大,矩形的长为_____,宽为_____.
=1的矩形面积最大,矩形的长为_____,宽为_____.
例1在边长为60 cm的正方形铁片的四角切去相等的正方形,再把它的边沿虚线折起(如图),做成一个无盖的方底箱子,箱底的边长是多少时,箱底的容积最大?最大容积是多少?
解法一:设箱底边长为xcm,则箱高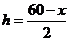 cm,得箱子容积
cm,得箱子容积
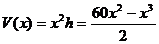
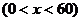 .
.
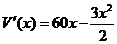
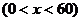
令 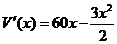 =0,解得 x=0(舍去),x=40,
=0,解得 x=0(舍去),x=40,
并求得 V(40)=16 000
由题意可知,当x过小(接近0)或过大(接近60)时,箱子容积很小,因此,16 000是最大值
答:当x=40cm时,箱子容积最大,最大容积是16 000cm3
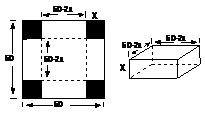 解法二:设箱高为xcm,则箱底长为(60-2x)cm,则得箱子容积
解法二:设箱高为xcm,则箱底长为(60-2x)cm,则得箱子容积
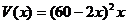
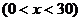 .(后面同解法一,略)
.(后面同解法一,略)
由题意可知,当x过小或过大时箱子容积很小,所以最大值出现在极值点处.
事实上,可导函数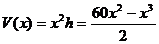 、
、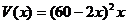 在各自的定义域中都只有一个极值点,从图象角度理解即只有一个波峰,是单峰的,因而这个极值点就是最值点,不必考虑端点的函数值
在各自的定义域中都只有一个极值点,从图象角度理解即只有一个波峰,是单峰的,因而这个极值点就是最值点,不必考虑端点的函数值
例2圆柱形金属饮料罐的容积一定时,它的高与底与半径应怎样选取,才能使所用的材料最省?
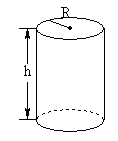 解:设圆柱的高为h,底半径为R,则表面积
解:设圆柱的高为h,底半径为R,则表面积
S=2πRh+2πR2
由V=πR2h,得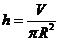 ,则
,则
S(R)= 2πR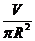 +
2πR2=
+
2πR2=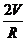 +2πR2
+2πR2
令 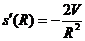 +4πR=0
+4πR=0
解得,R=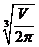 ,从而h=
,从而h=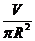 =
=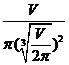 =
=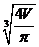 =2
=2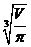
即 h=2R
因为S(R)只有一个极值,所以它是最小值
答:当罐的高与底直径相等时,所用材料最省
变式:当圆柱形金属饮料罐的表面积为定值S时,它的高与底面半径应怎样选取,才能使所用材料最省?
提示:S=2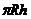 +
+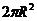
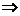 h=
h=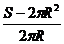
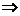 V(R)=
V(R)=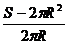
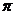 R
R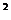 =
=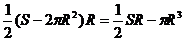
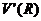 )=0
)=0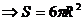
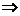
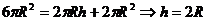 .
.
1 解决实际应用问题时,要把问题中所涉及的几个变量转化函数关系式,这需要通过分析,联想,抽象和转化完成,函数的最值要由极值和端点的函数值确定,当定义域是开区间且函数只有一个极值时,这个极值就是它的最值。
2.实际应用问题的解题程序:
1读题 2建模 3求解 4反馈
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com