
4.解有约束条件的排列问题的方法有直接法、间接法、元素位置分析法、插空法、捆绑法、枚举法、对称法、隔板法.
3.n个不同元素全部取出的一个排列,叫做n个不同元素的一个全排列,全排列数用Ann表示,它等于自然数从1到n的连乘积,自然数从1到n的连乘积叫做n的阶乘,用 表示.
2.从n个不同元素中取出m(m≤n)个元素的所有排列的个数,叫做从 个为不同元素中取出m个元素的排列数,用符号Amn表示.排列数公式Amn= .
个为不同元素中取出m个元素的排列数,用符号Amn表示.排列数公式Amn= .
这里m≤n,其中等式的右边是 个连续的自然数相乘,最大的是 ,最小的是 .
1.一般地说,从n个不同元素中,任取m(m≤n)个元素,按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列.
排列的定义包含两个基本内容:一是“取出元素”;二是“按照一定顺序排列”.因此当元素完全相同,并且元素的排列顺序也完全相同时,才是同一个排列.
3.解题方法:枚举法、插空法、隔板法.
|
例1. 高三(1)、(2)、(3)班分别有学生48,50,52人
(1) 从中选1人当学生代表的方法有多少种?
(2) 从每班选1人组成演讲队的方法有多少种?
(3) 从这150名学生中选4人参加学代会有多少种方法?
(4) 从这150名学生中选4人参加数理化四个课外活动小组,共有多少种方法?
解:(1)48+50+52=150种 (2)48×50×52=124800种 (3)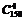 (4)
(4)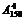
变式训练1:在直角坐标x-o-y平面上,平行直线x=n,(n=0,1,2,3,4,5),y=n,(n=0,1,2,3,4,5),组成的图形中,矩形共有( )
A、25个 B、36个 C、100个 D、225个
解:在垂直于x轴的6条直线中任意取2条,在垂直于y轴的6条直线中任意取2条,这样的4 条直线相交便得到一个矩形,所以根据分步记数原理知道:
得到的矩形共有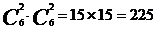 个,
故选D。
个,
故选D。
例2. (1) 将5封信投入6个信箱,有多少种不同的投法?
(2) 设I={1,2,3,4,5,6},A与B都是I的子集,A∩B={1,3,5},则称(A,B)为理想配,所有理想配共有多少种?
(3) 随着电讯事业的发展,许多地方电话号码升位,若某地由原来7位电话号码升为8位电话号码,问升位后可多装多少门电话机?(电话号码首位不为0)
解:(1)65 (2)27 (3)电话号码首位不为0:9×107-9×106=8.1×107
变式训练2:一个圆分成6个大小不等的小扇形,取来红、黄、兰、白、绿、黑6种颜色。
请问:⑴6个小扇形分别着上6种颜色有多少种不同的着色方法?
⑵从这6种颜色中任选5种着色,但相邻两个扇形不能着相同的颜色, 则有
多少种不同的着色方法?
解:⑴6个小扇形分别着上6种不同的颜色,共有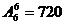 种着色方法.
种着色方法.
⑵6个扇形从6种颜色中任选5种着色共有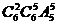 种不同的方法;其中相邻两个扇形是同一种颜色的着色方法共有
种不同的方法;其中相邻两个扇形是同一种颜色的着色方法共有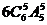 ;因此满足条件的着色方法共有
;因此满足条件的着色方法共有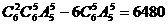 种着色方法.
种着色方法.
例3. 如图A,B,C,D为海上的四个小岛,现在要建造三座桥,将这四个小岛连接起来,则不同的建桥方案有( )
 D
D
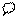 A
A
A、8种 B、12种 C、16种 D、20种
 B C
B C
解:第一类:从一个岛出发向其它三岛各建一桥,共有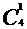 =4种方法;
=4种方法;
第二类:一个岛最多建设两座桥,例如:A-B-C-D,D-C-B-A,这样的两个排列对应一种建桥方法,因此有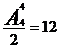 种方法;
种方法;
根据分类计数原理知道共有4+12=16种方法
变式训练3:某公司招聘进8名员工,平均分给下属的甲、乙两个部门,其中两名翻译人员不能同时分给一个部门,另三名电脑编程人员也不能同时分给一个部门,求有多少种不同的分配方案.
解:用分步计数原理.先分英语翻译,再分电脑编程人员,最后分其余各人,故有2×(3+3)×3=36种.
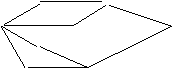
例4. 如图,小圆圈表示网络的结点,结点之间的连线表示它们有网线相连,连线上标注的数字表示该段网线单位时间内可以通过的最大信息量,现从结点A向结点B传递信息,信息可以沿不同的路径同时传递,则单位时间传递的最大信息量是( )
A、26 B、24 C、20 D、19
 3
3  5
5  12
12
B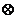 4
4 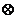 6
6 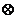 A
A
6 7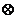 6 12
6 12
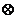 8
8 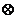
解:要完成的这件事是:“从A向B传递信息”,完成这件事有4类办法:

 第一类:12 5 3
第一类:12 5 3

 第二类 : 12 6 4
第二类 : 12 6 4

 第三类 :12 6 7
第三类 :12 6 7

 第四类;:12 8 6
第四类;:12 8 6
可见:第一类中单位时间传递的最大信息量是3;第二类单位时间传递的最大信息量是4;
第三类单位时间传递的最大信息量是6;第四类单位时间传递的最大信息量是6。所以由分类记数原理知道共有:3+4+6+6=19,故选D
变式训练4:7个相同的小球,任意放入4个不同的盒子,则每个盒子都不空的放法有多少种?
解:首先要清楚:“每个盒子都不空”的含义是“每个盒子里至少有1个球”。
于是,我们采用“隔板法”来解决。在7个小球中的每两个之间分别有6个空,我们从6个空中任意选3个分别插入3块隔板,则这3块隔板就把7个小球分成4部分,而且每一部分至少有1个球。即有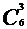 =20种方法,又每一种分割方法都对应着一种放球的放法。所以共有20种放球放法。
=20种方法,又每一种分割方法都对应着一种放球的放法。所以共有20种放球放法。
注;(1)本题若采取“分类讨论”的方法来解决,则显得很麻烦;大家可以试一试。
(2)隔板法只能用于“各个元素不加区别”的情况,否则不能使用.
两个原理的区别在于,前者每次得到的是最后的结果,后者每次得到的是中间结果,即每次仅完成整件事情的一部分,当且仅当几个步骤全部做完后,整件事情才算完成.
第2课时 排 列
|
2.分步计数原理(也称乘法原理):做一件事情,完成它需要分成n个步骤,做第一步有m1种不同的方法,做第二步有m2种不同的方法,……,做n步有mn种不同的方法,那么完成这件事共有N= 种不同的方法.
1.分类计数原理(也称加法原理):做一件事情,完成它可以有n类办法,在第一类办法中有m1种不同的方法,在第二类办法中有m2种不同的方法,……,在第n类办法中有mn种不同的方法,那么完成这件事共有N= 种不同的方法.
4.掌握二项式定理和二项展开式的性质,并能用它们计算和证明一些简单的问题.
|
|
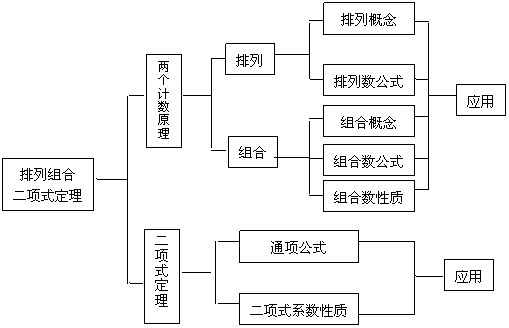
排列与组合高考重点考察学生理解问题、综合运用分类计数原理和分步计数原理分析问题和解决问题的能力及分类讨论思想.它是高中数学中从内容到方法都比较独特的一个组成部分,是进一步学习概率论的基础知识.由于这部分内容概念性强,抽象性强,思维方法新颖,同时解题过程中极易犯“重复”或“遗漏”的错误,而且结果数目较大,无法一一检验,因此学生要学好本节有一定的难度.解决该问题的关键是学习时要注意加深对概念的理解,掌握知识的内在联系和区别,严谨而周密地去思考分析问题.
二项式定理是进一步学习概率论和数理统计的基础知识,高考重点考查展开式及通项,难度与课本内容相当.另外利用二项式定理及二项式系数的性质解决一些较简单而有趣的小题,在高考中也时有出现.
第1课时 两个计数原理
|
3.理解组合的意义,掌握组合数计算公式和组合数性质,并能用它们解决一些简单的应用问题.
2.理解排列的意义,掌握排列数计算公式,并能用它解决一些简单的应用问题.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com