1．(a+b)ⁿ＝　　　　　 (n∈N)，这个公式称做二项式定理，右边的多项式叫做(a+b)ⁿ的二项展开式，其中的系数　　　 叫做二项式系数．式中的　　　　　 叫做二项展开式的通项，用T_r+1表示，即通项公式T_r+1＝　　　　 是表示展开式的第r+1项．

3．对于用直接法解较难的问题时，则采用间接法解.

2．排列组合应用题题形多变，但首先要弄清是有序还是无序，这是一个核心问题.

1．排列组合应用题的背景丰富无特定的模式和规律可循，背景陌生时，必须认真审题，把握问题的本质特征，并善于把问题转化为排列组合的常规模式进而求解.

4．对于有多个约束条件的问题，先应该深入分析每个约束条件，再综合考虑如何分类或分步，但对于综合性较强的问题则需要交叉使用两个原理来解决问题.

例1. 五个人站成一排，求在下列条件下的不同排法种数：

(1)甲必须在排头；

(2)甲必须在排头，并且乙在排尾；

(3)甲、乙必须在两端；

(4)甲不在排头，并且乙不在排尾；

(5)甲、乙不在两端；

(6)甲在乙前；

(7)甲在乙前，并且乙在丙前；

(8)甲、乙相邻；

(9)甲、乙相邻，但是与丙不相邻；

(10)甲、乙、丙不全相邻

解析：(1)特殊元素是甲，特殊位置是排头；首先排“排头”有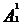种，再排其它4个位置有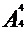种，所以共有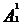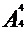：×=24种

(2)甲必须在排头，并且乙在排尾的排法种数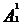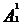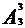：××=6种

(3)首先排两端有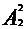种，再排中间有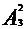种，

所以甲、乙必须在两端排法种数为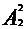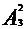：×=12种

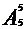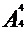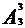(4)甲不在排头，并且乙不在排尾排法种数为：－2+=78种

(5)因为两端位置符合条件的排法有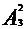种，中间位置符合条件的排法有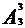种，

所以甲、乙不在两端排法种数为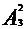×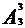=36种

(6)因为甲、乙共有2！种顺序，所以甲在乙前排法种数为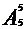：÷2！=60种

(7)因为甲、乙、丙共有3！种顺序，

所以甲在乙前，并且乙在丙前排法种数为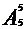：÷3！=20种

(8)把甲、乙看成一个人来排有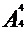种，而甲、乙也存在顺序变化，所以甲、乙相邻排法种数为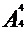×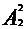=48种

(9)首先排甲、乙、丙外的两个有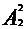，从而产生3个空，把甲、乙看成一个人与丙插入这3个空中的两个有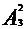，而甲、乙也存在顺序变化，所以甲、乙相邻，但是与丙不相邻排法种数为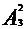××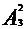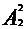=24种

(10)因为甲、乙、丙相邻有×，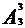

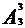所以甲、乙、丙不全相邻排法种数为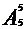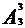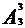－×=84种

变式训练1：某栋楼从二楼到三楼共10级，上楼只许一步上一级或两级，若规定从二楼到三楼用8步走完，则不同的上楼方法有　　　　　　　　　　　　　 (　 )

A．45种　　　　 B．36种　

C．28种　　　　 D．25种

解：C.　 8步走10级，则其中有两步走两级，有6步走一级．一步走两级记为a，一步走一级记为b，所求转化为2个a和6个b排成一排，有多少种排法．故上楼的方法有C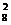＝28种；或用插排法．

例2. (1) 某校从8名教师中选派4名教师同时去4个远地区支教(每地1人)，其中甲和乙不同去，甲和丙只能事去或同不去，则不同的选派方案菜有多少处？

(2) 5名乒乓选手的球队中，有2名老队员和3名新队员，现从中选出3名队员排成1、2、3号参加团体比赛，则入选的3名队员中至少有一名老队员，且1、2号中至少有1名新队员的排法有多少种？

解：(1)分类：第一为甲丙都去，第二类不去共有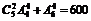种

(2)分类：第一类两名老队员都去，第二类去一名老队员共有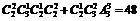种

变式训练2：某班新年联欢会原定的六个节目已安排成节目单，开演前又增加了三个新节目，如果将这三个节目插入原来的节目单中，那么不同的插法种数是　　　 (　 )

A．504　　　　　 B．210　

C．336　　　　　 D．120

解：A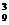＝504 故选A　

例3. 已知直线ax+by+c=0中的系数a，b，c是从集合{-3，-2，-1，0，1，2，3}中取出的三个不同的元素，且该直线的倾斜角为锐角，请问这样的直线有多少条？

解：首先把决定“直线条数”的特征性质，转化为对“a，b，c”的情况讨论。

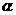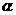设直线的倾斜角为，并且为锐角。

则tan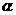=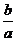－＞0,不妨设a＞b,那么b＜0

当c≠0时,则a有3种取法,b有3种取法,c有4种取法,并且其中任意两条直线不重合,所以这样的直线有3×3×4=36条

当c=0时, a有3种取法,b有3种取法, 其中直线:3x-3y=0,2x-2y=0,x-y=0重合,所以这样的直线有3×3-2=7条

故符合条件的直线有7+36=43条

变式训练3：将5名大学生毕业生分配到某公司所属的三个部门中去，要求每个部门至少分配一人，则不同的分配方案共有______种.

解：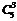

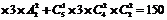
例4. 从集合{1，2，3，……20}中任选3个不同的数，使这3个数成等差数列，这样的等差数列可以有多少个？

解：a，b，c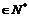　 a，b，c成等差数列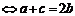　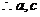 要么同为奇数，要么同为偶数，故满足题设的等差数列共有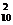A+A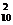＝180(个)

变式训练4：某赛季足球比赛中的计分规则是：胜一场得3分，平一场得1分，负一场得0分，一球 队打完15场，积33分，若不考虑顺序，该队胜负平的情况共有多少种？

解：设该队胜负平的情况是：胜x场，负y场，则平15－(x+y)场，依题意有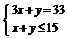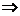：x≥9 。故有3种情况，即胜、负、平的场数是：9，0，6；10，2，3；11，4，0．

3．处理排列组合综合性问题时一般方法是先取(选)后排，但有时也可以边取(选)边排.

2．解排列组合综合题一般要遵循以下的两个原则(1)按元素性质进行分类(2)按事情发生的过程进行分步.

1．解排列组合题中常用的方法有直接法、间接法、两个原理、元素位置分析法、捆绑法、插空法、 枚举法、隔板法、对称法；常用的数学思想主要有分类讨论、思想转化、化归思想、对应思想.

4．避免重复和遗漏．

第4课时　　 排列组合综合题

3．组合问题的一般可抽象为“选派”模型来处理．另外有的问题也可用框图结合对应思想来处理。