
4.设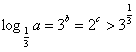 ,则( )
,则( )
A.a>c>b B.b>a>c C.c>b> a D.b>c> a
3.在同一平面直角坐标系中,函数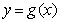 的图象与
的图象与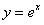 的图象关于直线
的图象关于直线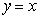 对称,而
对称,而
函数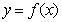 的图象与
的图象与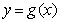 的图象关于
的图象关于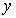 轴对称,若
轴对称,若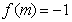 ,则
,则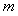 的值是( )
的值是( )
A.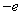 B.
B.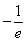 C.
C.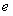 D.
D.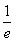
2.条件p: a<-2;条件q:函数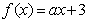 在区间[-1,2]上存在
在区间[-1,2]上存在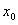 ,使得
,使得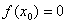 成立.
成立.
则p是q的( )
A.必要不充分条件 B.充分不必要条件 C.充分必要条件 D.既不充分也不必要条件
1.设集合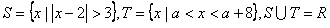 ,则
,则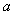 的取值范围是( )
的取值范围是( )
A.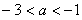 B.
B.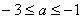 C.
C.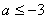 或
或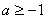 D.
D. 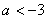 或
或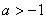
4.求余数或证明整除问题,被除数是幂指数问题时,解决问题的关键是将底数转化为除数的倍数加1或减1.通过练习要仔细地去体会其中的变形技巧.
3.应用二项式定理计算一个数的乘方的近似值时,应根据题设中对精确度的要求,决定展开式中各项的取舍.
2.二项式的展开式中二项式系数与项的系数是两个不同的概念,前者仅与二项式的指数及项数有关,与二项式无关,后者与二项式,二项式的指数及项数均有关.
1.注意(a+b)n及(a-b)n展开式中,通项公式分别为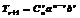 及
及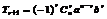 这里
这里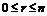 且展开式都有n+1项,在使用时要注意两个公式的区别,求二项式的展开式中的指定项,要扣住通项公式来解决问题.
且展开式都有n+1项,在使用时要注意两个公式的区别,求二项式的展开式中的指定项,要扣住通项公式来解决问题.
3.二项式定理主要有以下应用
①近似计算
②解决有关整除或求余数问题
③用二项式定理证明一些特殊的不等式和推导组合公式(其做法称为“赋值法”)
注意二项式定理只能解决一些与自然数有关的问题
④ 杨辉三角形

例1. (1) (06湖南理11)若(ax-1)5的展开式中x3的系数是-80,则实数a的值是 .
(2) (06湖北文8)在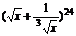 的展开式中,x的幂指数是整数的有
项.
的展开式中,x的幂指数是整数的有
项.
(3) (1+x)+(1+x)2+(1+x)3+……+(1+x)6展开式中x2项的系数为 .
解:(1)-2 (2)5项 (3)35
变式训练1:若多项式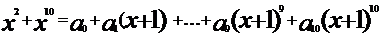 , 则
, 则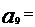 ( )
( )
A、9 B、10 C、-9 D、-10
解:根据左边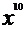 的系数为1,易知
的系数为1,易知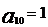 ,左边
,左边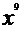 的系数为0,右边
的系数为0,右边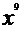 的系数为
的系数为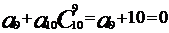 ,∴
,∴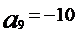 故选D。
故选D。
例2. 已知f(x)=(1+x)m+(1+x)n,其中m、n∈N展开式中x的一次项系数为11,问m、n为何值时,含x3项的系数取得最小值?最小值是多少?
由题意 ,则含x3项的系数为
,则含x3项的系数为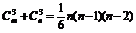 +
+

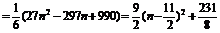 ,当n=5或6时x3系数取得最小值为30
,当n=5或6时x3系数取得最小值为30
变式训练2:分已知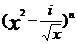 的展开式中第三项与第五项的系数之比为
的展开式中第三项与第五项的系数之比为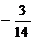 ,其中
,其中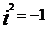 ,则展开式中常数项是( )
,则展开式中常数项是( )
A、 -45i B、 45i C、 -45 D、45
解析: 第三项,第五项的系数分别为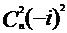 ,
,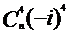
依据题意有: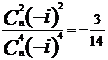 ,
,
整理得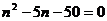
即解方程(n-10)(n+5)=0
则只有n=10适合题意.由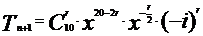 ,
,
当 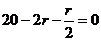 时,有r=8,
时,有r=8,
故常数项为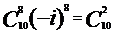 =45 故选D
=45 故选D
例3. 若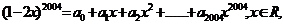 求(
求(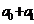 )+(
)+(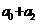 )+……+(
)+……+( )
)
解:对于式子: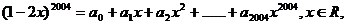
令x=0,便得到: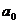 =1
=1
令x=1,得到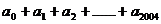 =1
=1
又原式:(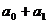 )+(
)+(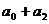 )+……+(
)+……+(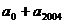 )
)
=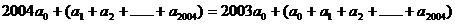
∴原式:(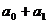 )+(
)+(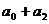 )+……+(
)+……+(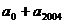 )=2004
)=2004
注意:“二项式系数”同二项式展开式中“项的系数”的区别与联系.
变式训练3:若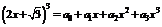 ,则
,则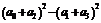 的值是 ( )
的值是 ( )
A.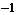 B.1
B.1
C.0 D.2
解:A
例4. 已知二项式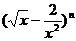 ,(n∈N
,(n∈N )的展开式中第5项的系数与第3项的系数的
)的展开式中第5项的系数与第3项的系数的
比是10:1,
(1)求展开式中各项的系数和
(2)求展开式中系数最大的项以及二项式系数最大的项
解:(1)∵第5项的系数与第3项的系数的比是10:1,
∴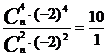 ,解得n=8
,解得n=8
令x=1得到展开式中各项的系数和为(1-2) =1
=1
(2) 展开式中第r项, 第r+1项,第r+2项的系数绝对值分别为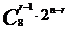 ,
,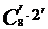 ,
,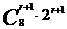 ,
,
若第r+1项的系数绝对值最大,则必须满足:
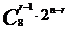 ≤
≤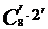 并且
并且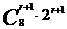 ≤
≤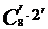 ,解得5≤r≤6;
,解得5≤r≤6;
所以系数最大的项为T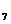 =1792
=1792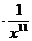 ;二项式系数最大的项为T
;二项式系数最大的项为T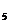 =1120
=1120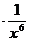
变式训练4:①已知(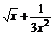 )n的第5项的二项式系数与第三项的二项系数的比是14:3,求展开式中不含x的项.
)n的第5项的二项式系数与第三项的二项系数的比是14:3,求展开式中不含x的项.
②求(x-1)-(x-1)2+(x-1)3-(x-1)4+(x-1)5的展开式中x2项的系数.
解: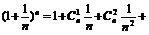
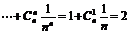
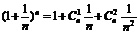
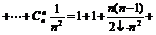
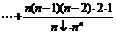

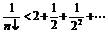
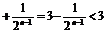
|
2.二项式定理中,二项式系数的性质有:
① 在二项式展开式中,与首末两项“等距离”的两项二项式系数相等,即:
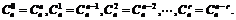
② 如果二项式的幂指数是偶数,中间一项的二项式系数最大;如果二项式的幂指数是奇数,中间两项的二项式系数相等并且最大,即当n是偶数时,n+1是奇数,展开式共有n+1项,中间一项,即:
第 项的二项式系数最大,为 ;当n是奇数时,n+1是偶数,展开式共有n+1项,中间两项,即第 项及每 项,它们的二项式系数最大,为
③ 二项式系数的和等于---------,即------------
④ 二项展开式中,偶数项系数和等于奇数项的系数和= 即
⑤ 展开式中相邻两项的二项式系数的比是:
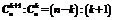
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com