
7.若双曲线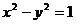 的左支上一点P(a,b)到直线
的左支上一点P(a,b)到直线
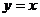 的距离为
的距离为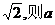 +b的值为
( A )
+b的值为
( A )
A.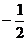 B.
B.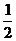 C.-2 D.2
C.-2 D.2
6.已知函数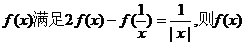 的最小
的最小
值是 A.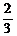 B.2 C.
B.2 C.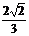 D.
D.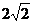 ( C )
( C )
5.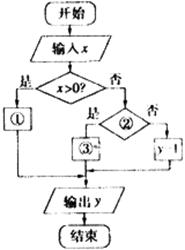 函数
函数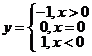 的程序框图如图所示,
的程序框图如图所示,
则①②③的填空能完全正确的是: (D)
A. ①y=0; ②x=0;③y=1; B. ①y=0;②x<0;③y=1;
C. ①-1;②x>0;③y=0; D. ①y=-1;②x=0;③y=0.
4.若等比数列{an}对一切正整数n都有Sn=2an-1,其中 Sn是{an}的前n项和,则公比q的值
为 A.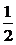 B.-
B.-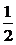 C.2
D.-2
( C
)
C.2
D.-2
( C
)
3.已知直线a、b与平面α,给出下列四个命题
①若a∥b,b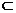 α,则a∥α; ②若a∥α,b
α,则a∥α; ②若a∥α,b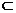 α,则a∥b ;
α,则a∥b ;
③若a∥α,b∥α,则a∥b; ④a⊥α,b∥α,则a⊥b.
其中正确的命题是 A.1个 B.2个 C.3个 D.4个 ( A )
1.准线方程为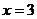 的抛物线的标准方程为 ( B )
的抛物线的标准方程为 ( B )
A.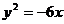 B.
B.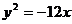 C.
C.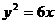 D.
D.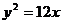
2 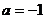 是直线
是直线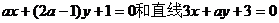 垂直的 ( A )
垂直的 ( A )
A.充分不必要的条件 B.必要不充分的条件 C.充要条件 D.既不充分又不必要条件
18.(1)证法1:∵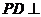 平面
平面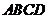 ,
,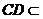 平面
平面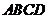 ,∴
,∴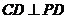 .
.
又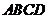 为正方形,∴
为正方形,∴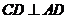 .∵
.∵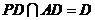 ,∴
,∴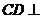 平面
平面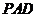 .
.
∵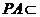 平面
平面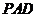 ,∴
,∴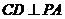 .∵
.∵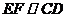 ,∴
,∴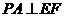 .
.
证法2:以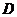 为原点,建立如图所示的空间直角坐标系
为原点,建立如图所示的空间直角坐标系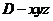 ,
,
则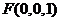 ,
,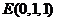 ,
,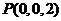 ,
,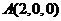 ,
,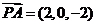 ,
,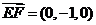 .
.
 ∵
∵ ,∴
,∴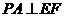 .
.
(2)解法1:以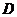 为原点,建立如图所示的空间直角坐标系
为原点,建立如图所示的空间直角坐标系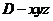 ,
,
则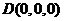 ,
,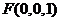 ,
,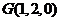 ,
,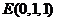 ,
,
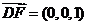 ,
,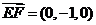 ,
,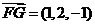 .
.
设平面DFG的法向量为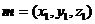 ,∵
,∵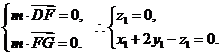
令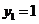 ,得
,得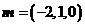 是平面
是平面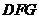 的一个法向量.
的一个法向量.
设平面EFG的法向量为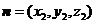 ,∵
,∵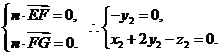
令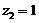 ,得
,得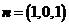 是平面
是平面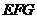 的一个法向量.
的一个法向量.
∵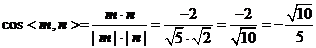 .
.
设二面角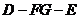 的平面角为θ,则
的平面角为θ,则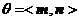 .
.
所以二面角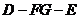 的余弦值为
的余弦值为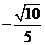 .
.
解法2:以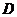 为原点,建立如图所示的空间直角坐标系
为原点,建立如图所示的空间直角坐标系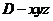 ,
,
则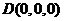 ,
,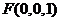 ,
,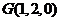 ,
,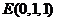 ,
,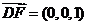 ,
,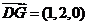 ,
,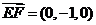 ,
,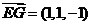 ,
,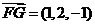 .………………………………8分
.………………………………8分
 过
过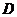 作
作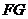 的垂线,垂足为
的垂线,垂足为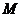 ,
,
∵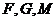 三点共线,∴
三点共线,∴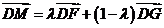 ,
,
∵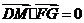 ,∴
,∴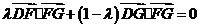 ,
,
即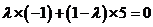 ,解得
,解得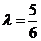 .
.
∴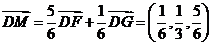 .…………10分
.…………10分
再过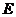 作
作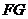 的垂线,垂足为
的垂线,垂足为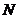 ,
,
∵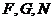 三点共线,∴
三点共线,∴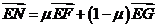 ,
,
∵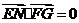 ,∴
,∴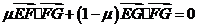 ,
,
即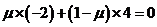 ,解得
,解得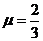 .
.
∴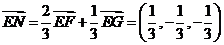 .∴
.∴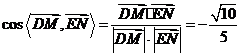 .
.
∵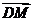 与
与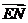 所成的角就是二面角
所成的角就是二面角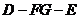 的平面角,
的平面角,
所以二面角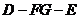 的余弦值为
的余弦值为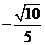 .
.
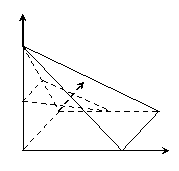
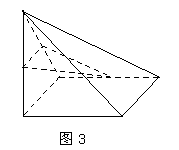
18.如图3所示,四棱锥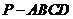 中,底面
中,底面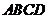 为正方形,
为正方形,
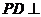 平面
平面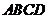 ,
,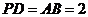 ,
, ,
,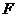 ,
,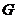 分别为
分别为
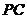 、
、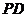 、
、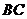 的中点.
的中点.
(1)求证: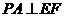 ;
;
(2)求二面角D-FG-E的余弦值.
17. 将棱长为3的正四面体以各顶点截去四个棱长为1的小正四面体(使截面平行于底面),所得几何体的表面积为
将棱长为3的正四面体以各顶点截去四个棱长为1的小正四面体(使截面平行于底面),所得几何体的表面积为
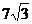 。
。
16.过椭圆的左焦点F且倾斜角为60°的直线交椭圆于A,B两点,若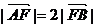 ,则椭圆的离心率e=
,则椭圆的离心率e= 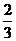 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com